题目内容
14.已知集合A={x∈Z|-1≤x≤2},B={x|log3x<1},则A∩B=( )| A. | {-1,0,1,2} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |
分析 分别求出集合A中的元素,求出集合B,取交集即可.
解答 解:A={x∈Z|-1≤x≤2}={-1,0,1,2},
B={x|log3x<1}={x|0<x<3},
则A∩B={1,2},
故选:D.
点评 本题考查了集合的交集的运算,考查解不等式问题,是一道基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
5.函数f(x)=lnx+x2-bx+a(b>0,a∈R)的图象在点(b,f(b))处的切线斜率的最小值是( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 2 |
19.若a,b∈{-1,1,2,3},则直线ax+by=0与圆x2+(y+2)2=2有交点的概率为( )
| A. | $\frac{3}{8}$ | B. | $\frac{11}{16}$ | C. | $\frac{5}{8}$ | D. | $\frac{5}{16}$ |
6.已知实数x,y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y-2≤0\end{array}\right.$,函数f(x)=logc(x+2)-1(c>0,c≠1)的图象恒过定点A(a,b),则$z=\frac{y-b}{x-a}$的取值范围是( )
| A. | $[\frac{1}{3},2]$ | B. | $[\frac{2}{5},1]$ | C. | $[\frac{1}{2},\frac{3}{2}]$ | D. | $[\frac{3}{2},\frac{5}{2}]$ |
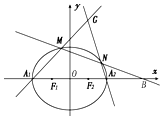 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点. 如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.
如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.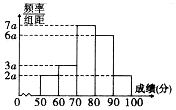 在某市举办的安全教育知识竞赛中,抽取1800名学生的成绩(单位:分),其频率分布直方图如图所示,则成绩落在[50,60)中的学生人数为180.
在某市举办的安全教育知识竞赛中,抽取1800名学生的成绩(单位:分),其频率分布直方图如图所示,则成绩落在[50,60)中的学生人数为180.