题目内容
16.在△ABC中,角A,B,C所对的边分别为a,b,c,若1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$,则A=( )| A. | 30°? | B. | 45°? | C. | 60°? | D. | 120°? |
分析 由同角三角函数基本关系式,正弦定理,两角和的正弦函数公式化简已知可求cosA,结合A的范围,由特殊角的三角函数值即可求解.
解答 解:∵1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$,
∴1+$\frac{sinAcosB}{cosAsinB}$=$\frac{2sinC}{sinB}$,可得:$\frac{cosAsinB+sinAcosB}{cosAsinB}$=$\frac{2sinC}{sinB}$,
∴$\frac{sinC}{cosAsinB}$=$\frac{2sinC}{sinB}$,
∴cosA=$\frac{1}{2}$,
∵A∈(0°,180°),
∴A=60°.
故选:C.
点评 本题主要考查了同角三角函数基本关系式,正弦定理,两角和的正弦函数公式,特殊角的三角函数值在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知实数x,y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y-2≤0\end{array}\right.$,函数f(x)=logc(x+2)-1(c>0,c≠1)的图象恒过定点A(a,b),则$z=\frac{y-b}{x-a}$的取值范围是( )
| A. | $[\frac{1}{3},2]$ | B. | $[\frac{2}{5},1]$ | C. | $[\frac{1}{2},\frac{3}{2}]$ | D. | $[\frac{3}{2},\frac{5}{2}]$ |
11.设 (1+i)( x-yi)=2,其中 x,y 是实数,i 为虚数单位,则 x+y=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
1.已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<2\\ f(x-1),x≥2\end{array}\right.$则f(log27)=$\frac{7}{2}$.
8.要得到函数 y=2cos x 的图象,只需将 y=2sin( x-$\frac{π}{3}$) 的图象( )
| A. | 向右平移$\frac{5π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{5π}{6}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
3.如果函数y=logax(a>0且a≠1)在[1,3]上的最大值与最小值的差为2,则满足条件的a值的集合是( )
| A. | $\{\sqrt{3}\}$ | B. | $\{\frac{{\sqrt{3}}}{3}\}$ | C. | $\{\frac{{\sqrt{3}}}{3},\sqrt{3}\}$ | D. | $\{\sqrt{3},3\}$ |
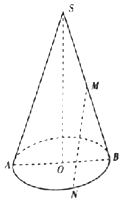 如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6.
如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6.