题目内容
19.已知抛物线y2=4x截直线y=2x+m所得弦长$|{AB}|=\sqrt{15}$.(1)求m的值;
(2)设P是x轴上的点,且△ABP的面积为$\frac{{9\sqrt{3}}}{2}$,求点P的坐标.
分析 (1)将直线方程代入抛物线方程,由韦达定理及弦长公式可知$|{AB}|=\sqrt{15}$.即可求得m的值;
(2)由直线AB的方程,利用点到直线的距离公式求得$d=\frac{{|{2a-1}|}}{{\sqrt{5}}}$,利用三角形的面积公式,即可求得点P的坐标.
解答 解:(1)将直线方程代入抛物线方程$\left\{{\begin{array}{l}{y=2x+m}\\{{y^2}=4x}\end{array}}\right.$,
整理得4x2+4(m-1)x+m2=0.
设A(x1,y1),B(x2,y2),则有x1+x2=1-m,${x_1}{x_2}=\frac{m^2}{4}$.
于是$|{AB}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|$=$\sqrt{1+{2^2}}\sqrt{{{({1-m})}^2}-4×\frac{m^2}{4}}$=$\sqrt{5({1-2m})}$.
因为$|{AB}|=\sqrt{15}$,
所以$\sqrt{5({1-2m})}$=$\sqrt{15}$,解得m=-1.
∴m的值-1;
(2)设P(a,0),P到直线AB的距离为d,
因为lAB:2x-y+m=0,由点到直线的距离公式得$d=\frac{{|{2a-1}|}}{{\sqrt{5}}}$,
又${S_{△ABP}}=\frac{1}{2}|{AB}|•d$,所以$d=\frac{{2{S_{△ABP}}}}{{|{AB}|}}$,
于是$\frac{{|{2a-1}|}}{{\sqrt{5}}}=\frac{{2×\frac{{9\sqrt{3}}}{2}}}{{\sqrt{15}}}$,
解得a=5或a=-4,
故点P的坐标为(5,0)或(-4,0).
点评 本题考查直线与抛物线的位置关系,韦达定理,弦长公式及三角形的面积公式,考查计算能力,属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
| A. | 向右平移$\frac{5π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{5π}{6}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
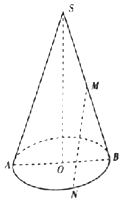 如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6.
如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6.