题目内容
12.给出命题:若方程mx2+ny2=1(m,n∈R)表示椭圆,则mn>0.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 根据椭圆的定义判断原命题的真假,从而求出逆否命题的真假,求出逆命题的真假,从而判断出否命题的真假即可.
解答 解:若方程mx2+ny2=1(m,n∈R)表示椭圆,则m>0,n>0,故mn>0,
故原命题是真命题,逆否命题是真命题,
若mn>0,则方程mx2+ny2=1(m,n∈R)表示椭圆,是假命题,
故否命题是假命题,
故选:B.
点评 本题考查了四种命题的关系,考查椭圆的定义,是一道基础题.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
20.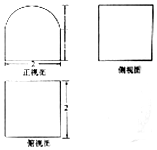 某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
 某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )| A. | 12+3π | B. | 10+3π | C. | 12+4π | D. | 10+4π |
17.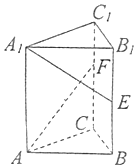 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )
 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )| A. | $-\frac{{\sqrt{2}}}{6}$ | B. | $\frac{{\sqrt{2}}}{6}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
 如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.
如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.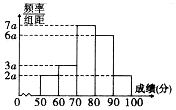 在某市举办的安全教育知识竞赛中,抽取1800名学生的成绩(单位:分),其频率分布直方图如图所示,则成绩落在[50,60)中的学生人数为180.
在某市举办的安全教育知识竞赛中,抽取1800名学生的成绩(单位:分),其频率分布直方图如图所示,则成绩落在[50,60)中的学生人数为180.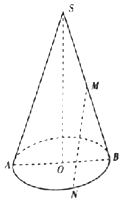 如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6.
如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6.


 如图古铜钱外圆内方,外圆直径为4cm,中间是边长为1cm的正方形孔,随机地在古铜钱所在圆内任取一点,则该点刚好位于孔中的概率是$\frac{1}{4π}$.
如图古铜钱外圆内方,外圆直径为4cm,中间是边长为1cm的正方形孔,随机地在古铜钱所在圆内任取一点,则该点刚好位于孔中的概率是$\frac{1}{4π}$.