题目内容
9.已知函数f(x)=|x+1|+|2x-4|.(Ⅰ)解关于x的不等式f(x)<9;
(Ⅱ)若直线y=m与曲线y=f(x)围成一个三角形,求实数m的取值范围,并求所围成的三角形面积的最大值.
分析 (Ⅰ)分类讨论以去掉绝对值号,即可解关于x的不等式f(x)<9;
(Ⅱ)作出函数的图象,结合图象求解.
解答 解:(Ⅰ)x≤-1,不等式可化为-x-1-2x+4<9,∴x>-2,∴-2<x≤-1;
-1<x<2,不等式可化为x+1-2x+4<9,∴x>-4,∴-1<x<2;
x≥2,不等式可化为x+1+2x-4<9,∴x<4,∴2≤x<4;
综上所述,不等式的解集为{x|-2<x<4};
(Ⅱ)f(x)=|x+1|+2|x-2|,
由题意作图如下,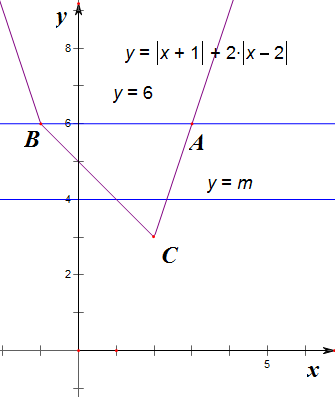 ,
,
结合图象可知,A(3,6),B(-1,6),C(2,3);
故3<m≤6,
且m=6时面积最大为$\frac{1}{2}$×(3+1)×3=6.
点评 本题考查了绝对值函数的应用及数形结合的思想方法应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.若a,b∈{-1,1,2,3},则直线ax+by=0与圆x2+(y+2)2=2有交点的概率为( )
| A. | $\frac{3}{8}$ | B. | $\frac{11}{16}$ | C. | $\frac{5}{8}$ | D. | $\frac{5}{16}$ |
20.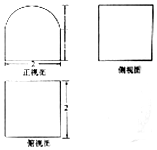 某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
 某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )| A. | 12+3π | B. | 10+3π | C. | 12+4π | D. | 10+4π |
17.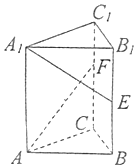 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )
 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )| A. | $-\frac{{\sqrt{2}}}{6}$ | B. | $\frac{{\sqrt{2}}}{6}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
14.若 x,y 满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y-4≤0\\ y≥0\end{array}\right.$,则 z=y-2x 的最大值为( )
| A. | 8 | B. | 4 | C. | 1 | D. | 2 |
1.已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<2\\ f(x-1),x≥2\end{array}\right.$则f(log27)=$\frac{7}{2}$.
18.已知a,b是两条不同的直线,α是平面,且b?α,那么“a∥α”是“a∥b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知命题p:函数y=lg(1-x)在(-∞,1)上单调递减,命题q:函数y=2cosx是偶函数,则下列命题中为真命题的是( )
| A. | p∧q | B. | (¬p)∨(¬q) | C. | (¬p)∧q | D. | p∧(¬q) |