题目内容
甲、乙两人玩掷骰子游戏:甲先掷一个骰子,记下向上的点数;然后乙再掷,同样记下向上的点数.如果两人所掷点数之和为偶数则甲胜,否则乙获胜.
(Ⅰ)求甲胜且点数之和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?用你所学的知识说明理由.
(Ⅰ)求甲胜且点数之和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?用你所学的知识说明理由.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(I)计算出两人的投掷结果的情况总数,及甲胜且点数之和为6的情况个数,代入古典概型概率计算公式,可得答案.
(II)分别计算甲乙两人获胜的概率,比较后可得游戏是否公平.
(II)分别计算甲乙两人获胜的概率,比较后可得游戏是否公平.
解答:
解:(I)设“甲胜且点数之和为6”为事件A,甲乙的点数分别为x,y,
则两人的投掷结果共有6×6=36个基本事件,
其中事件A包括的基本事件共有:
(1,5),(2,4),(3,3),(4,2),(5,1)共5个基本事件,
∴P(A)=
,
∴甲胜且点数之和为6的事件发生的概率为
.
(Ⅱ)这种游戏公平.
设“甲胜”为事件B,“乙胜”为事件C.甲胜即两个点数的和为偶数.
所包含基本事件为以下18个:
(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),
(3,1),(3,3),(3,5),(4,2),(4,4),(4,6),
(5,1),(5,3)(5,5),(6,2),(6,4),(6,6)…(10分)
所以甲胜的概率为P(B)=
=
;
乙胜的概率为P(C)=
=
,
∴P(B)=P(C)所以这种游戏是公平的 (13分)
则两人的投掷结果共有6×6=36个基本事件,
其中事件A包括的基本事件共有:
(1,5),(2,4),(3,3),(4,2),(5,1)共5个基本事件,
∴P(A)=
| 5 |
| 36 |
∴甲胜且点数之和为6的事件发生的概率为
| 5 |
| 36 |
(Ⅱ)这种游戏公平.
设“甲胜”为事件B,“乙胜”为事件C.甲胜即两个点数的和为偶数.
所包含基本事件为以下18个:
(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),
(3,1),(3,3),(3,5),(4,2),(4,4),(4,6),
(5,1),(5,3)(5,5),(6,2),(6,4),(6,6)…(10分)
所以甲胜的概率为P(B)=
| 18 |
| 36 |
| 1 |
| 2 |
乙胜的概率为P(C)=
| 18 |
| 36 |
| 1 |
| 2 |
∴P(B)=P(C)所以这种游戏是公平的 (13分)
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
相关题目
已知不同直线m,n和不同平面α,β,给出下列命题:
①若α∥β,m?α,则m∥β;
②若m∥n,n⊥β,m?α,则α⊥β;
③若α∥m,β∥m,则α∥β;
④若α⊥β,m∥α,则m⊥β.
其中的真命题有( )
①若α∥β,m?α,则m∥β;
②若m∥n,n⊥β,m?α,则α⊥β;
③若α∥m,β∥m,则α∥β;
④若α⊥β,m∥α,则m⊥β.
其中的真命题有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
(
+
)5展开式的常数项为80,则a的值为( )
| x |
| a | |||
|
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
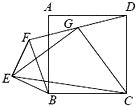 如图,四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF.连接DF,G为DF的重点,连接EG,CG,EC,求证:|
如图,四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF.连接DF,G为DF的重点,连接EG,CG,EC,求证:|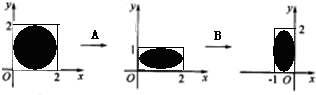 二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.
二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.