题目内容
等差数列{an}的前n项和为Sn,已知它的公差不等于零,S3=a22,且S1,S2,S4成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=anan+1,求数列{
}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)设bn=anan+1,求数列{
| 1 |
| bn |
考点:数列的求和,等差数列的性质,等比数列的性质
专题:等差数列与等比数列
分析:(1)设数列{an}的公差为d,由已知条件利用等差数列通项公式和前n项和公式及等比数列性质,求出首项和公差,由此能求出an=2n-1.
(2)由bn=anan+1=(2n-1)(2n+1),得
=
=
(
-
),由此利用裂项求和法能求出数列{
}的前n项和Tn.
(2)由bn=anan+1=(2n-1)(2n+1),得
| 1 |
| bn |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| bn |
解答:
解:(1)设数列{an}的公差为d,
由S3=a22,得3a2=a22,解得a2=0或a2=3,
∵S1,S2,S4成等比数列,∴S22=S1S4,
∴(2a1+d)2=a1(4a1+6d),
化简,得d(d-2a1)=0,
∵d≠0,∴d=2a1,
由
,得
,
∴an=2n-1.
(2)∵bn=anan+1=(2n-1)(2n+1),
∴
=
=
(
-
),
∴Tn=
(1-
+
-
+…+
-
)
=
(1-
)
=
.
由S3=a22,得3a2=a22,解得a2=0或a2=3,
∵S1,S2,S4成等比数列,∴S22=S1S4,
∴(2a1+d)2=a1(4a1+6d),
化简,得d(d-2a1)=0,
∵d≠0,∴d=2a1,
由
|
|
∴an=2n-1.
(2)∵bn=anan+1=(2n-1)(2n+1),
∴
| 1 |
| bn |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
=
| n |
| 2n+1 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)=|x-1|,求f(3)=( )
| A、1 | B、2 | C、3 | D、4 |
给定两个命题p和q,若p是¬q的充分而不必要条件,则¬p是q的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,在圆心角为直角的扇形OAB中,随机投入一点,则该点落入三角形区域(阴影部分)的概率为( )
如图,在圆心角为直角的扇形OAB中,随机投入一点,则该点落入三角形区域(阴影部分)的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
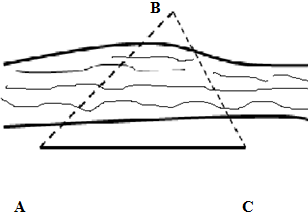 如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.
如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.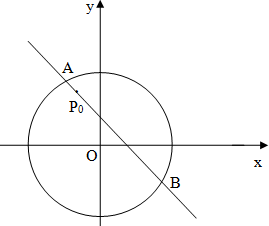 如图,圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.
如图,圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.