题目内容
已知数列{an}满足an+an+1=6n+1(n∈N*)
(1)若{an}是等差数列,求数列{an}的通项公式;
(2)若数列{an}满足a1=3,Sn是数列{an}的前n项的和,设bn=
,是否存在正整数k,使得
<b2+b4+…+b2k<
?若存在,求出所有的k值;若不存在,请说明理由.
(1)若{an}是等差数列,求数列{an}的通项公式;
(2)若数列{an}满足a1=3,Sn是数列{an}的前n项的和,设bn=
| 2 |
| 2Sn+5n |
| 1 |
| 8 |
| 1 |
| 7 |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件得an+2-an=6,由此能求出an=3n-1.
(2)由已知条件得数列{an}的奇数项是首项为3,公差为6的等差数列,偶数项是首项为4,公差为6的等差数列,从而得到b2+b4+…+b2k=
(1-
+
-
+…+
-
)=
,由此能示出存在正整数k,k=4,5.
(2)由已知条件得数列{an}的奇数项是首项为3,公差为6的等差数列,偶数项是首项为4,公差为6的等差数列,从而得到b2+b4+…+b2k=
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| k |
| 1 |
| k+1 |
| k |
| 6(k+1) |
解答:
(本题满分13分)
解:(1)∵an+an+1=6n+1,
∴an+1+an+2=6n+7,∴an+2-an=6,
又数列{an}是等差数列,设其公差为d,则2d=6,∴d=3,…(3分)
又a1+a2=7,∴2a1+d=7,∴a1=2,∴an=2+3(n-1)=3n-1,
故数列{an}的通项公式为an=3n-1(n∈N*).…(6分)
(2)由 a1+a2=7,又a1=3,得a2=4,
由(1)知数列{an}的奇数项是首项为3,公差为6的等差数列,
偶数项是首项为4,公差为6的等差数列.…(8分)
S2k=3k+
×6+4k+
×6=6k2+k,
∴b2k=
=
=
=
(
-
)…(10分)
∴b2+b4+…+b2k=
(1-
+
-
+…+
-
)=
,
解不等式
<
<
,得3<k<6
又k为正整数,故存在正整数k,k=4,5.…(13分)
解:(1)∵an+an+1=6n+1,
∴an+1+an+2=6n+7,∴an+2-an=6,
又数列{an}是等差数列,设其公差为d,则2d=6,∴d=3,…(3分)
又a1+a2=7,∴2a1+d=7,∴a1=2,∴an=2+3(n-1)=3n-1,
故数列{an}的通项公式为an=3n-1(n∈N*).…(6分)
(2)由 a1+a2=7,又a1=3,得a2=4,
由(1)知数列{an}的奇数项是首项为3,公差为6的等差数列,
偶数项是首项为4,公差为6的等差数列.…(8分)
S2k=3k+
| k(k-1) |
| 2 |
| k(k-1) |
| 2 |
∴b2k=
| 2 |
| 2S2k+10k |
| 2 |
| 12k2+12k |
| 1 |
| 6k(k+1) |
| 1 |
| 6 |
| 1 |
| k |
| 1 |
| k+1 |
∴b2+b4+…+b2k=
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| k |
| 1 |
| k+1 |
| k |
| 6(k+1) |
解不等式
| 1 |
| 8 |
| k |
| 6(k+1) |
| 1 |
| 7 |
又k为正整数,故存在正整数k,k=4,5.…(13分)
点评:本题考查数列的通项公式的求法,考查满足条件的正整数的求法,是中档题,解题时要注意挖掘隐含条件,注意裂项求和法的合理运用.

练习册系列答案
相关题目
函数y=x2cos2x的导数为( )
| A、y′=2xcos2x-x2sin2x |
| B、y′=2xcos2x-2x2sin2x |
| C、y′=x2cos2x-2xsin2x |
| D、y′=2xcos2x+2x2sin2x |
 如图,在圆心角为直角的扇形OAB中,随机投入一点,则该点落入三角形区域(阴影部分)的概率为( )
如图,在圆心角为直角的扇形OAB中,随机投入一点,则该点落入三角形区域(阴影部分)的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
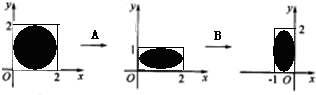 二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.
二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.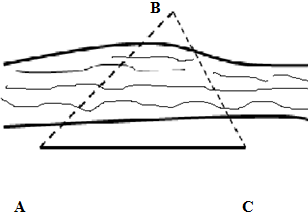 如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.
如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.