题目内容

已知等比数列{an}满足a1＞0，a1006=2，则log2a1+log2a2+log2a3+…+log2a2011=
 
．
考点：等比数列的性质
专题：等差数列与等比数列
分析：根据等比数列的性质和对数的运算性质即可得到结论．
解答： 解：在等比数列中a1＞0，a1006=2＞0，
∴an＞0，
∵log2a1+log2a2+log2a3+…+log2a2011=log2（a1a2…a2011），
∵a1006=2，
∴a1a2011=a2a2010=…=（a1006）2=4，
∴a1a2…a2011=41005×2=22011，
∴log2a1+log2a2+log2a3+…+log2a2011=log222011=2011，
故答案为：2011．
点评：本题主要考查对数的运算和等比数列的性质，考查学生的计算能力．
练习册系列答案
相关题目
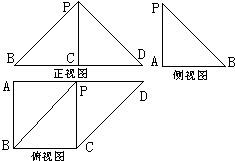如图是一几何体的三视图，正视图是一等腰直角三角形，且斜边BD长为2；侧视图为一直角三角形；俯视图为一直角梯形，且AB=BC=1，则此几何体的体积是（　　）
A、
1
2
B、
2
C、
2
2
D、1
选修4-1：几何证明选讲
如图，E是圆O中直径CF延长线上一点，弦AB⊥CF，AE交圆O于P，PB交CF于D，连接AO、AD．求证：
（Ⅰ）∠E=∠OAD；
（Ⅱ）OF2=OD•OE．
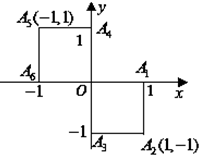小波以游戏方式决定：是去打球、唱歌还是去下棋．游戏规则为：以O为起点，再从A1，A2，A3，A4，A5，A6（如图）这6个点中任取两点分别为终点得到两个向量，记这两个向量的数量积为X，若X＞0就去打球；若X=0就去唱歌；若X＜0就去下棋．
（Ⅰ）分别求小波去下棋的概率和不去唱歌的概率．
（Ⅱ）写出数量积X的所有可能取值，并求X分布列与数学期望．
如果执行如图程序框图，那么输出的S=
 
．
正四棱锥的底面边长为2，侧棱长均为
3
，其正视图和侧视图是全等的等腰三角形，则正视图的周长为
 
．
三棱锥A-BCD中，BA⊥AD，BC⊥CD，且AB=1，AD=
3
，则此三棱锥外接球的体积为
 
．
若
a
=(1，λ，λ-λ2)，
b
=(2，1，
1
2
)，且
a
与
b
的夹角为锐角，则λ的取值范围为
 
．
已知圆（x-1）2+（y-3
3
）2=r2（r＞0）的一条切线y=kx+
3
与直线x=5的夹角为
π
6
，则半径r的值为（　　）
A、
3
2
B、
3
3
2
C、
3
2
 或
3
3
2
D、
3
2
或
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网