题目内容
△ABC的面积为
，BC=
，∠C=60°，则边AB的长度等于 ．
| 3 |
| 2 |
考点：正弦定理
专题：解三角形
分析：根据题意和三角形的面积公式先求出AC，再由余弦定理求出AB的值．
解答：
解：由题意得，△ABC的面积为
，BC=
，∠C=60°，
所以
AC•
•sin60°=
，解得AC=2
，
由余弦定理得，AB2=BC2+AC2-2•AC•BC•cosC
=2+8-2×2
×
×
=6，
所以AB=
，
故答案为：
．
| 3 |
| 2 |
所以
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
由余弦定理得，AB2=BC2+AC2-2•AC•BC•cosC
=2+8-2×2
| 2 |
| 2 |
| 1 |
| 2 |
所以AB=
| 6 |
故答案为：
| 6 |
点评：本题考查了余弦定理，以及三角形的面积公的应用，熟练掌握定理和公式是解题的关键．
练习册系列答案
ABC考王全优卷系列答案
相关题目
设f（x）=x2-4x（x∈R），则f（x）＜0的一个必要不充分条件是（ ）
| A、0＜x＜4 |
| B、x＜0或x＞4 |
| C、0≤x＜4 |
| D、0＜x＜3 |
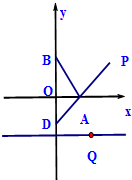如图，在平面直角坐标系中，O为坐标原点，点B（0，1），且点A（a，0）（a≠0）是x轴上动点，过点A作线段AB的垂线交y轴于点D，在直线AD上取点P，使AP=DA．在△ABC中，若
•（
-2
）=0，则△ABC的形状为 （ ）
| AB |
| AB |
| AC |
| A、直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |