题目内容
函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜
）的最小正周期为π，若其图象向右平移
个单位后得到的函数时奇函数，则函数f（x）的图象（ ）
| π |
| 2 |
| π |
| 6 |
A、在（0，
| ||
B、在（0，
| ||
C、关于直线x=
| ||
D、关于点（
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：依题意，可求得f（x）=sin（2x+
），利用正弦函数的性质，对A、B、C、D四个选项逐一分析即可得答案．
| π |
| 3 |
解答：
解：∵f（x）=sin（ωx+φ）（ω＞0，|φ|＜
）的最小正周期为π，
即T=
=π，故ω=2；
又f（x-
）=sin[2（x-
）+φ]=sin（2x-
+φ）为奇函数，
∴φ-
=kπ（k∈Z），
∴φ=kπ+
（k∈Z），又|φ|＜
，
∴φ=
，
∴f（x）=sin（2x+
）．
∵f（
）=
＞f（
）=0可排除A；
由
≤2x+
≤
得：
≤x≤
，即函数f（x）在[
，
]上单调递减，可排除B；
∵2×
+
=
，故函数f（x）的图象关于直线x=
对称，即C正确；
∵f（
）=sin（
+
）=-
≠0，可排除D；
故选：C．
| π |
| 2 |
即T=
| 2π |
| ω |
又f（x-
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
∴φ-
| π |
| 3 |
∴φ=kπ+
| π |
| 3 |
| π |
| 2 |
∴φ=
| π |
| 3 |
∴f（x）=sin（2x+
| π |
| 3 |
∵f（
| π |
| 6 |
| ||
| 2 |
| π |
| 3 |
由
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
| π |
| 12 |
| 7π |
| 12 |
∵2×
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
∵f（
| 5π |
| 12 |
| 5π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
故选：C．
点评：本题考查函数y=Asin（ωx+φ）的图象变换，突出考查正弦函数的单调性、对称性、考查综合分析、运算能力，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=x2+2x+1-2x，则y=f（x）的图象大致为（ ）
A、 |
B、 |
C、 |
D、 |
已知命题p：“若直线ax+y+1=0与直线ax-y+2=0垂直，则a=1”；命题q：“a
＞b
是a＞b”的充要条件，则（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、p真q假 | B、p且q真 |
| C、p或q真 | D、p或q假 |
命题p：a（a-1）≤0；命题q：y=xa（x为自变量）在第一象限是增函数，p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
如图所示是一个几何体的三视图，则这个几何体外接球的表面积为（ ）
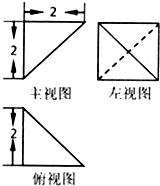
| A、8π | B、12π |
| C、16π | D、48π |
按照如图所示的算法框图，则输出的结果是（ ）
| A、1005 | B、1006 |
| C、1007 | D、1008 |
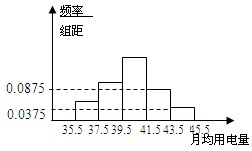某乡镇供电所为了调查农村居民用电量情况，随机抽取了500户居民去年的用电量（单位：kw/h），将所得数据整理后，画出频率分布直方图如下；其中直方图从左到右前3个小矩形的面积之比为1：2：3．