题目内容
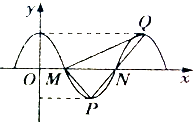已知函数f（x）=Acosωx（ω＞0）的部分图象如图所示，且∠MQP=| π |
| 6 |
| 3 |
（1）求MP的长；
（2）求函数f（x）的单调递减区间．
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质,解三角形
分析：（1）由图知，MP=PN=NQ，∠MQP=
，MQ=2
，利用余弦定理得MP2=MQ2+PQ2-2MQ•PQ•cos∠MQP，易求MP的长；
（2）依题意，可求得f（x）=
cos
，利用正弦函数的单调性，解不等式2kπ≤
≤2kπ+π，k∈Z，即可求得函数f（x）的单调递减区间．
| π |
| 6 |
| 3 |
（2）依题意，可求得f（x）=
| 3 |
| πx |
| 2 |
| πx |
| 2 |
解答：
解：（1）结合函数f（x）图象的对称性易知：MP=PN=NQ…（1分）
MP2=MQ2+PQ2-2MQ•PQ•cos∠MQP，
即x2=(2
)2+(2x)2-2×2
×2xcos
，…（3分）
整理得x2-4x+4=0，解得x=2，故所求MP=2…（5分）
（2）由（1）知MP=2，PQ=4，MQ=2
，所以MP2+MQ2=PQ2，所以△MPQ是直角三角形，且∠MPN=
..（6分）
又由MP=PN=2，∠MPN=
知，△MPN是边长为2的等边三角形…（7分）
所以MN=2，所以T=
=4，解得ω=
又点P到x轴的距离为
，所以A=
，于是函数f(x)=
cos
…（9分）
令2kπ≤
≤2kπ+π，k∈Z，解得4k≤x≤4k+2，k∈Z（…11分）
故函数f（x）的单调递减区间为[4k，4k+2]（k∈Z）…（14分）
MP2=MQ2+PQ2-2MQ•PQ•cos∠MQP，
即x2=(2
| 3 |
| 3 |
| π |
| 6 |
整理得x2-4x+4=0，解得x=2，故所求MP=2…（5分）
（2）由（1）知MP=2，PQ=4，MQ=2
| 3 |
| π |
| 3 |
又由MP=PN=2，∠MPN=
| π |
| 3 |
所以MN=2，所以T=
| 2π |
| ω |
| π |
| 2 |
又点P到x轴的距离为
| 3 |
| 3 |
| 3 |
| πx |
| 2 |
令2kπ≤
| πx |
| 2 |
故函数f（x）的单调递减区间为[4k，4k+2]（k∈Z）…（14分）
点评：本题考查余弦定理的应用，考查函数的周期性、对称性，突出考查正弦函数的单调性的应用，考查推理、识图与运算能力，属于中档题．
练习册系列答案
相关题目
设向量
，
是同一平面内所有向量的一组基底，若（λ
+
）∥（
-2
），则实数λ的值为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
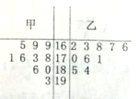甲、乙两名工人生产的零件尺寸记成如图所示的茎叶图，已知零件尺寸在区间[165，180]内的为合格品．（单位：mm）
已知函数f（x）=x2+2x+1-2x，则y=f（x）的图象大致为（ ）
A、 |
B、 |
C、 |
D、 |