题目内容
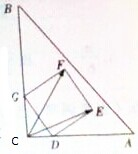如图放置的边长为1的正方形DEFG的顶点D，G分别在Rt△ABC的两直角边所在的直线上滑动，则| CE |
| CF |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：令∠OAD=θ，以CA为x轴的正半轴、CB为y轴正半轴，可得出E，F的坐标，由此可以表示出两个向量，算出它们的内积即可．
解答：
解：如图令∠CDG=θ，由于DG=1故CD=cosθ，CG=sinθ，
如图∠EDA=-θ，DE=1，故xE=cosθ+cos（-θ）=cosθ+sinθ，yE=sin（-θ）=cosθ，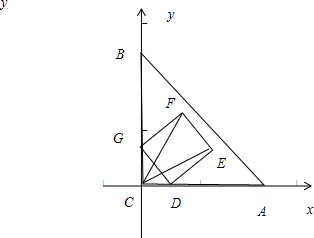
故
=（cosθ+sinθ，cosθ）
同理可求得F（sinθ，cosθ+sinθ），即
=（sinθ，cosθ+sinθ），
∴
•
=（cosθ+sinθ，cosθ）•（sinθ，cosθ+sinθ）=1+sin2θ，
故
•
的最大值是2，
故答案是 2．
如图∠EDA=-θ，DE=1，故xE=cosθ+cos（-θ）=cosθ+sinθ，yE=sin（-θ）=cosθ，
故
| CE |
同理可求得F（sinθ，cosθ+sinθ），即
| CF |
∴
| CE |
| CF |
故
| CE |
| CF |
故答案是 2．
点评：本题主要考查向量在几何中的应用，设角引入坐标是解题的关键，由于向量的运算与坐标关系密切，所以在研究此类题时应该想到设角来表示点的坐标，属于中档题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
