题目内容
已知函数f(x)=2sinxcosx-
cos2x.
(Ⅰ)求f(0)的值及函数f(x)的单调递增区间;
(Ⅱ)求函数f(x)在区间[0,
]上的最大值和最小值.
| 3 |
(Ⅰ)求f(0)的值及函数f(x)的单调递增区间;
(Ⅱ)求函数f(x)在区间[0,
| π |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由f(x)=sin2x-
cos2x=2sin(2x-
),得f(0)=-
.从而求出f(x)的单调递增区间;
(Ⅱ)由-
≤2x-
≤
.得出当x=0时,f(x)取得最小值,x=
时,f(x)取得最大值.
| 3 |
| π |
| 3 |
| 3 |
(Ⅱ)由-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 5π |
| 12 |
解答:
解:(Ⅰ)∵f(x)=sin2x-
cos2x=2sin(2x-
)
∴f(0)=-
.
由-
+2kπ≤2x-
≤
+2kπ,k∈Z,
得-
+kπ≤x≤
+kπ,k∈Z
∴f(x)的单调递增区间是[kπ-
,kπ+
],k∈Z.
(Ⅱ)∵0≤x≤
,
∴-
≤2x-
≤
.
∴当2x-
=-
,即x=0时,f(x)取得最小值-
;
当2x-
=
即x=
时,f(x)取得最大值2.
| 3 |
| π |
| 3 |
∴f(0)=-
| 3 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
得-
| π |
| 12 |
| 5π |
| 12 |
∴f(x)的单调递增区间是[kπ-
| π |
| 12 |
| 5π |
| 12 |
(Ⅱ)∵0≤x≤
| π |
| 2 |
∴-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴当2x-
| π |
| 3 |
| π |
| 3 |
| 3 |
当2x-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
点评:本题考查了函数的单调性,函数的最值问题,考查导数的应用,三角函数的应用,是一道综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
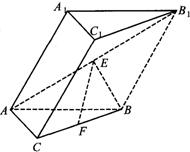 如图,在斜三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
如图,在斜三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
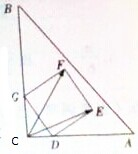 如图放置的边长为1的正方形DEFG的顶点D,G分别在Rt△ABC的两直角边所在的直线上滑动,则
如图放置的边长为1的正方形DEFG的顶点D,G分别在Rt△ABC的两直角边所在的直线上滑动,则