题目内容
已知平面α内有n个点，且任意三点都不共线，若“这n个点到平面β的距离均相等”是“α∥β”的充要条件，则n的最小值为 ．
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：利用平面间的位置关系求解．
解答：
解：∵不在同一条直线三点确定一个平面，
∴至少有三个．
当有三个点时，如果在平面β的异侧，则不成立；
当四个点时，如果在平面β的异侧，且均平行于平面β，也不成立，
当有五个点时成立．
∴“这n个点到平面β的距离均相等”是“α∥β”的充要条件，则n的最小值为5．
故答案为：5．
∴至少有三个．
当有三个点时，如果在平面β的异侧，则不成立；
当四个点时，如果在平面β的异侧，且均平行于平面β，也不成立，
当有五个点时成立．
∴“这n个点到平面β的距离均相等”是“α∥β”的充要条件，则n的最小值为5．
故答案为：5．
点评：本题考查满足条件的n的最小值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
如图，三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC，△ABC为等腰直角三角形，∠BAC=90°，且AB=AA1，E、F分别是CC1，BC的中点．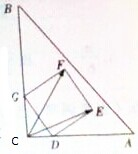
如图放置的边长为1的正方形DEFG的顶点D，G分别在Rt△ABC的两直角边所在的直线上滑动，则
某程序框图如图所示，现输入如下四个函数：f（x）=x2，f（x）=
用辗转相除法求49与91的最大公约数时的需要运算的次数为（ ）
| A、1次 | B、2次 | C、3次 | D、4次 |