题目内容
△ABC中，角A，B，C所对的边分别为a，b，c，已知cosA=
，△ABC面积为30．
（Ⅰ）求
•
；
（Ⅱ）若c-b=1时，求边a的值．
| 12 |
| 13 |
（Ⅰ）求
| AB |
| AC |
（Ⅱ）若c-b=1时，求边a的值．
考点：平面向量数量积的运算,正弦定理,余弦定理
专题：解三角形,平面向量及应用
分析：（1）利用平方关系可得sinA，再利用三角形的面积计算公式和数量积的定义即可得出；
（2）利用余弦定理即可得出．
（2）利用余弦定理即可得出．
解答：
解：（1）∵cosA=
，
∴sinA=
=
．
∵S△ABC=
bcsinA=30，
∴bc=156．
∴
•
=bccosA=156×
=144．
（2）由余弦定理可得a2=b2+c2-2bccosA=（b-c）2+2bc-2bccosA=25，
∴a=5．
| 12 |
| 13 |
∴sinA=
| 1-cos2A |
| 5 |
| 13 |
∵S△ABC=
| 1 |
| 2 |
∴bc=156．
∴
| AB |
| AC |
| 12 |
| 13 |
（2）由余弦定理可得a2=b2+c2-2bccosA=（b-c）2+2bc-2bccosA=25，
∴a=5．
点评：本题考查了平方关系、三角形的面积计算公式、数量积的定义、余弦定理，属于基础题．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
如图，三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC，△ABC为等腰直角三角形，∠BAC=90°，且AB=AA1，E、F分别是CC1，BC的中点．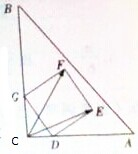
如图放置的边长为1的正方形DEFG的顶点D，G分别在Rt△ABC的两直角边所在的直线上滑动，则