题目内容
函数y=
的值域为 ．
| 8 |
| x2-4x+5 |
考点：函数的值域
专题：函数的性质及应用
分析：基本方法是配方法，显然y=
=
＞0，而（x-2）2+1的最小值为1，故y有最大值，最大值为8，问题得以解决．
| 8 |
| x2-4x+5 |
| 8 |
| (x-2)2+1 |
解答：
解：y=
=
＞0，
∵（x-2）2+1的最小值为1，当x=2时，取得最小值，
∴y有最大值，最大值为8，
故函数y=
的值域为（0，8]，
故答案为：（0，8]．
| 8 |
| x2-4x+5 |
| 8 |
| (x-2)2+1 |
∵（x-2）2+1的最小值为1，当x=2时，取得最小值，
∴y有最大值，最大值为8，
故函数y=
| 8 |
| x2-4x+5 |
故答案为：（0，8]．
点评：本题考查二次函数的值域的求法，较为基本，方法是配方法，配方法是高考考查的重点方法，学生要做到很熟练的对二次式进行配方．
练习册系列答案
名校课堂系列答案
相关题目
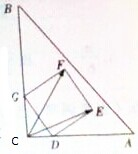如图放置的边长为1的正方形DEFG的顶点D，G分别在Rt△ABC的两直角边所在的直线上滑动，则
某程序框图如图所示，现输入如下四个函数：f（x）=x2，f（x）=