题目内容
已知函数y=1-2a-2ax+2x2(-1≤x≤1)的最小值为f(a),求f(a)的表达式,并指出当a∈[-3,0]时,函数M=log
f(a)的值域.
| 1 |
| 3 |
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:先确定函数的对称轴和开口方向,由于函数要求最小值,需分三种情形讨论,最后最小值写成分段函数的形式可得函数f(a);欲求M=log
f(a)的值域,根据对数函数的性质,关键是求当a∈[-2,0]时,f(a)的取值范围,结合二次函数的性质即可解决.
| 1 |
| 3 |
解答:
解:∵y=1-2a-2ax+2x2=2(x-
)2-
-2a+1,(-1≤x≤1),
当
<-1,即a<-2时,ymin=y|x=-1=f(a)=3;
当-1≤
≤1,即-2≤a≤2时,ymin=y|x=
=f(a)=-
a2-2a+1;
当
>1,即a>2时,ymin=y|x=1=f(a)=3-4a,2(x-
)2-
-2a+111
∴f(a)=
当a∈[-2,0]时,M=log
f(a)=log
(-
a2-2a+1),
设u=-
a2-2a+1=-
(a+2)2+3,a∈[-2,0],则1≤u≤3,
此时M=log
u∈[-1,0].
函数M=log
f(a)的值域为[-1,0].
| a |
| 2 |
| a2 |
| 2 |
当
| a |
| 2 |
当-1≤
| a |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
当
| a |
| 2 |
| a |
| 2 |
| a2 |
| 2 |
∴f(a)=
|
当a∈[-2,0]时,M=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
设u=-
| 1 |
| 2 |
| 1 |
| 2 |
此时M=log
| 1 |
| 3 |
函数M=log
| 1 |
| 3 |
点评:本题考查了二次函数的图象和性质,特别是求二次函数的最值,需要分类讨论,做到不重不漏,解题时要学会用分类讨论的思想方法解决问题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
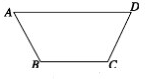 设计一个水渠,其横截面为等腰梯形(如图所示),要求满足条件AB+BC+CD=a(常数),∠ABC=120°,写出横截面的面积y与腰长x的关系式,并求它的定义域和值.
设计一个水渠,其横截面为等腰梯形(如图所示),要求满足条件AB+BC+CD=a(常数),∠ABC=120°,写出横截面的面积y与腰长x的关系式,并求它的定义域和值.