题目内容
函数f(x)=
是定义在(-1,1)上的奇函数,且f(
)=
.
(1)确定函数f(x)的解析式.
(2)用定义证明f(x)在(-1,1)上是增函数.
(3)在(2)的条件下,解不等式f(a2-1)+f(2a-1)<0.
| ax+b |
| 1+x2 |
| 1 |
| 2 |
| 2 |
| 5 |
(1)确定函数f(x)的解析式.
(2)用定义证明f(x)在(-1,1)上是增函数.
(3)在(2)的条件下,解不等式f(a2-1)+f(2a-1)<0.
考点:奇偶性与单调性的综合,利用导数研究函数的单调性
专题:函数的性质及应用
分析:(1)根据函数是奇函数,可得f(0)=0,再根据f(
)=
,列出关于a,b的方程组,求出即可得解析式;
(2)用函数单调性定义证明,任取x1,x2∈(-1,1),且x1<x2,f(x1)-f(x2)作差与0比较,从而证明函数的单调性.
(3)根据函数的单调性建立不等式关系即可得到结论.
| 1 |
| 2 |
| 2 |
| 5 |
(2)用函数单调性定义证明,任取x1,x2∈(-1,1),且x1<x2,f(x1)-f(x2)作差与0比较,从而证明函数的单调性.
(3)根据函数的单调性建立不等式关系即可得到结论.
解答:
解:(1)∵f(x)是奇函数,
∴f(-x)=-f(x)
即
=-
,
则-ax+b=-ax-b,
∴b=-b,即b=0,(或直接利用f(0)=0,解得b=0).
∴f(x)=
,
∵f(
)=
.∴f(
)=
=
,解得a=1,
∴f(x)=
.
(2)f(x)在(-1,1)上是增函数.
证明如下:任取x1,x2∈(-1,1),且x1<x2,
f(x1)-f(x2)=
-
=
,
∵-1<x1<x2<1,
∴-1<x1x2<1,x1-x2<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(-1,1)上是增函数.
(3)∵函数f(x)是奇函数,
∴不等式f(a2-1)+f(2a-1)<0等价为不等式f(a2-1)<-f(2a-1),
即f(a2-1)<f(1-2a),
∵f(x)在(-1,1)上是增函数.
∴
,
则
,即
,
解得0<a<
-1,即不等式的解集为(0,
-1).
∴f(-x)=-f(x)
即
| -ax+b |
| x2+1 |
| ax+b |
| x2+1 |
则-ax+b=-ax-b,
∴b=-b,即b=0,(或直接利用f(0)=0,解得b=0).
∴f(x)=
| ax |
| x2+1 |
∵f(
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 2 |
| ||
|
| 2 |
| 5 |
∴f(x)=
| x |
| x2+1 |
(2)f(x)在(-1,1)上是增函数.
证明如下:任取x1,x2∈(-1,1),且x1<x2,
f(x1)-f(x2)=
| x1 | ||
|
| x2 | ||
|
| (x1-x2)(1-x1x2) |
| (x12+1)(x22+1) |
∵-1<x1<x2<1,
∴-1<x1x2<1,x1-x2<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(-1,1)上是增函数.
(3)∵函数f(x)是奇函数,
∴不等式f(a2-1)+f(2a-1)<0等价为不等式f(a2-1)<-f(2a-1),
即f(a2-1)<f(1-2a),
∵f(x)在(-1,1)上是增函数.
∴
|
则
|
|
解得0<a<
| 3 |
| 3 |
点评:本题主要考查函数奇偶性和单调性的判断和应用,综合考查函数性质的应用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
函数f(x)=2sin(ωx+φ)(ω>0)的图象经过A(-
,-2)、B(
,2)两点,则ω( )
| π |
| 6 |
| π |
| 4 |
| A、最大值为3 | ||
| B、最小值为3 | ||
C、最大值为
| ||
D、最小值为
|
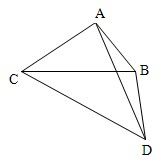 在三棱锥A-BCD中,平面ACB⊥平面BCD.在等腰直角三角形ABC中,AC=AB,AC=6,在Rt△BCD中,BC⊥BD,∠BCD=30°
在三棱锥A-BCD中,平面ACB⊥平面BCD.在等腰直角三角形ABC中,AC=AB,AC=6,在Rt△BCD中,BC⊥BD,∠BCD=30° AB是⊙O的直径,C为圆上一点,AB=2,AC=1,P为⊙O所在平面外一点,且PA⊥⊙O,PB与平面所成角为45°
AB是⊙O的直径,C为圆上一点,AB=2,AC=1,P为⊙O所在平面外一点,且PA⊥⊙O,PB与平面所成角为45°