题目内容
在△ABC中,a,b,c分别是内角A,B,C的对边,且(2a-c)cosB-bcosC=0.
(1)求∠B;
(2)设函数f(x)=-2cos(2x+B),将f(x)的图象向左平移
后得到函数g(x)的图象,求函数g(x)的单调递增区间.
(1)求∠B;
(2)设函数f(x)=-2cos(2x+B),将f(x)的图象向左平移
| π |
| 12 |
考点:正弦定理
专题:解三角形
分析:(1)已知等式利用正弦定理化简,整理后再利用诱导公式、两角和的正弦公式变形,求出cosB的值,即可确定出∠B的大小;
(2)根据三角函数图象平移法则、诱导公式求出g(x),再由正弦函数的单调递增区间、整体思想,求出函数g(x)的单调递增区间.
(2)根据三角函数图象平移法则、诱导公式求出g(x),再由正弦函数的单调递增区间、整体思想,求出函数g(x)的单调递增区间.
解答:
解:(1)由(2a-c)cosB-bcosC=0及正弦定理得,
(2sinA-sinC)cosB-sinBcosC=0,
即2sinAcosB-sin(B+C)=0,
因为A+B+C=π,所以sin(B+C)=sinA,
因为sinA≠0,所以cosB=
,
由B是三角形内角得,B=
,
(2)由(1)得,B=
,
则f(x)=-2cos(2x+B)=-2cos(2x+
),
所以g(x)=-2cos[2(x+
)+
],
=-2cos(2x+
)=2sin2x,
由2kπ-
≤2x≤2kπ+
(k∈Z)得,kπ-
≤x≤kπ+
(k∈Z),
故函数g(x)的单调递增区间是:[kπ-
,kπ+
](k∈Z).
(2sinA-sinC)cosB-sinBcosC=0,
即2sinAcosB-sin(B+C)=0,
因为A+B+C=π,所以sin(B+C)=sinA,
因为sinA≠0,所以cosB=
| 1 |
| 2 |
由B是三角形内角得,B=
| π |
| 3 |
(2)由(1)得,B=
| π |
| 3 |
则f(x)=-2cos(2x+B)=-2cos(2x+
| π |
| 3 |
所以g(x)=-2cos[2(x+
| π |
| 12 |
| π |
| 3 |
=-2cos(2x+
| π |
| 2 |
由2kπ-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
故函数g(x)的单调递增区间是:[kπ-
| π |
| 4 |
| π |
| 4 |
点评:本题主要考查正弦定理,诱导公式、两角和的正弦公式,以及正弦函数的单调性的应用,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
设f(x)=
x3+ax2+5x+6在区间[1,3]上为单调递减函数,则实数a的取值范围为( )
| 1 |
| 3 |
A、(-∞,-
| ||||
| B、(-∞,-3] | ||||
C、(-∞,-3]∪[-
| ||||
D、(-
|
甲、乙、丙、丁、戊和己6名学生进行劳动技术比赛,决出第一到第六名的名次.甲、乙两名参赛者去询问成绩,回答者对甲说“很遗憾,你和乙都没有得到冠军”,对乙说“你当然不会是最差的”.从上述回答分析,6人的名次排列可能有( )种不同情况.
| A、180 | B、288 |
| C、384 | D、480 |
一物体的运动方程为S=6t2+3t-2,则它在t=3时的瞬时速度为( )
| A、36 | B、39 | C、12 | D、33 |
“m<
”是“方程x2+x+m=0有实数解”的( )
| 1 |
| 4 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
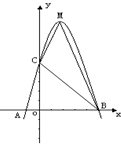 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.