Question

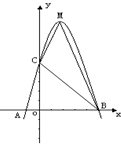已知：如图，二次函数y=ax²+bx+c的图象与x轴交于A、B两点，其中A点坐标为（-1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．
（1）求抛物线的解析式；
（2）求△MCB的面积S_△MCB．

Answer 1

考点：二次函数的性质

专题：函数的性质及应用

分析：（1）由A，C，D三点在抛物线上，代入函数y=ax²+bx+c的解析式，构造方程组，解得抛物线的解析式；
（2）过点M作平行与y轴的直线交BC于N，则△MCB的面积=△MCN的面积+△MNB的面积=

1

2

MN•OB．

解答： 解：（1）∵A（-1，0），C（0，5），D（1，8）在二次函数y=ax²+bx+c的图象上，
∴

a-b+c=0 c=5 a+b+c=8

，
解得：

a=-1 b=4 c=5

，
∴抛物线的解析式为y=-x²+4x+5，
（2）过点M作平行与y轴的直线交BC于N，
∵B点的坐标为：（5，0），
∴BC的方程为：

x

5

+

y

5

=1，当x=2，y=3，
故N点的坐标为（2，3），
函数y=-x²+4x+5的顶点为（2，9），则MN=6，
∴△MCB的面积=△MCN的面积+△MNB的面积=

1

2

MN•OB=15．

点评：本题考查的知识点是二次函数的图象和性质，三角形的面积，是二次函数图象与性质比较综合的应用，难度中档．