题目内容

图中表示的区域满足不等式（　　）
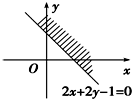
A、2x+2y-1＞0
B、2x+2y-1≥0
C、2x+2y-1≤0
D、2x+2y-1＜0
考点：二元一次不等式（组）与平面区域
专题：不等式的解法及应用
分析：先判断原点所在的区域，即可得到结论．
解答： 解：当x=0，y=0时，2x+2y-1=-1＜0，
即原点O在不等式2x+2y-1＜0对应的平面区域内，
∴图象中对应的平面区域满足不等式2x+2y-1≥0，
故选：B．
点评：本题主要考查二元一次不等式表示平面区域，利用原点进行判断是解决本题的关键，比较基础．
练习册系列答案
相关题目
在平面直角坐标系上，设不等式组
x＞0
y＞0
y≤-n(x-3)
所表示的平面区域为Dn，记Dn内的整点（即横坐标和纵坐标均为整数的点）的个数为an（n∈N*）．则a1=
 
，经推理可得到an=
 
．
若x、y满足条件
2x-y-1≤0
2x+y+1≥0
y≤x+1
，则z=x+3y的最大值是
 
．
给出下列命题：①若函数f(x)=
(3a-1)x+4a，x＜1
logax，x≥1
在（-∞，+∞）上是减函数，则a的取值范围是(0，
1
3
)；②若函数f（x）满足f（x+1）=f（3-x），则f（x）的图象关于直线x=2对称；③函数y=f（x+1）与函数y=f（3-x）的图象关于直线x=2对称；④若函数f（x+2013）=x2-2x-1（x∈R），则f（x）的最小值为-2．其中正确命题的序号有
 
（把所有正确命题的序号都写上）．
复数1+
3
i与复数-
3
+i在复平面上的对应点分别是A，B，O为坐标，则∠AOB等于（　　）
A、
π
6
B、
π
4
C、
π
3
D、
π
2
已知|
a
|=1，|
b
|=2，向量
a
与
b
的夹角为60°，则|
a
+
b
|=（　　）
A、
5
B、
7
C、1
D、2
已知实数x，y满足
x-2y+1≥0
|x|-y-1≤0
，则z=2x+y的最大值为（　　）
A、4B、6C、8D、10
任取三个整数，至少有一个数为偶数的概率为（　　）
A、0.125B、0.25
C、0.5D、0.875
在△ABC中，角A、B、C所对的边分别为a、b、c，己知
m
=（cosA，
3
sinA），
n
=（2cosA，-2cosA），
m
•
n
=-1．
（Ⅰ）若a=2
3
，c=2，求△ABC的面积；
（Ⅱ）求
b-2c
acos(60°+C)
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网