题目内容
给出下列命题:①若函数f(x)=
在(-∞,+∞)上是减函数,则a的取值范围是(0,
);②若函数f(x)满足f(x+1)=f(3-x),则f(x)的图象关于直线x=2对称;③函数y=f(x+1)与函数y=f(3-x)的图象关于直线x=2对称;④若函数f(x+2013)=x2-2x-1(x∈R),则f(x)的最小值为-2.其中正确命题的序号有 (把所有正确命题的序号都写上).
|
| 1 |
| 3 |
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:利用函数的单调性判断①的正误;利用函数的图象的对称性判断②的正误;利用两个函数的图象的对称性判断③的正误;利用二次函数的最值以及函数的图象的左右平移不改变函数的最值判断④的正误;
解答:
解:对于①,函数f(x)=
在(-∞,+∞)上是减函数,
∴a∈(0,1),并且3a-1<0,解得a<
,
3a-1+4a≥0,解得a≥
,
∴a∈[
,
),
∴①不正确;
对于②,函数f(x)满足f(x+1)=f(3-x),则f(x)的图象关于直线x=2对称,
∴②正确;
对于③,函数y=f(x+1)与函数y=f(3-x)的图象关于直线x=2对称;
∵函数y=f(a+x)与函数y=f(b-x)的图象关于直线x=
对称,
∴函数y=f(x+2)的图象与函数y=f(3-x)的图象关于直线x=
=1对称,
∴③不正确.
对于④,函数f(x+2013)=x2-2x-1=(x-1)2-2≥-2,函数的最小值是-2,则f(x)与f(x+2013)只是函数的图象左右平移,不改变函数的最小值为-2.
∴④正确.
综上正确是命题是:②④.
故答案为:②④.
|
∴a∈(0,1),并且3a-1<0,解得a<
| 1 |
| 3 |
3a-1+4a≥0,解得a≥
| 1 |
| 7 |
∴a∈[
| 1 |
| 7 |
| 1 |
| 3 |
∴①不正确;
对于②,函数f(x)满足f(x+1)=f(3-x),则f(x)的图象关于直线x=2对称,
∴②正确;
对于③,函数y=f(x+1)与函数y=f(3-x)的图象关于直线x=2对称;
∵函数y=f(a+x)与函数y=f(b-x)的图象关于直线x=
| b-a |
| 2 |
∴函数y=f(x+2)的图象与函数y=f(3-x)的图象关于直线x=
| 3-1 |
| 2 |
∴③不正确.
对于④,函数f(x+2013)=x2-2x-1=(x-1)2-2≥-2,函数的最小值是-2,则f(x)与f(x+2013)只是函数的图象左右平移,不改变函数的最小值为-2.
∴④正确.
综上正确是命题是:②④.
故答案为:②④.
点评:本题考查函数的图象的单调性,函数的最值,考查函数图象的对称性,要求区分f(a+x)=f(a-x)与y=f(a+x)和y=f(a-x)的对称性是区别,前者关于x=a对称,后者关于y轴对称.

练习册系列答案
相关题目
已知△ABC是正三角形,且它的边长为a,那么它的直观图△A′B′C′的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
图中表示的区域满足不等式( )
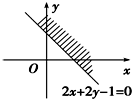

| A、2x+2y-1>0 |
| B、2x+2y-1≥0 |
| C、2x+2y-1≤0 |
| D、2x+2y-1<0 |
下列说法中,正确的是( )
| A、数据 5,4,4,3,5,2 的众数是 4 |
| B、一组数据的标准差是这组数据的方差的平方 |
| C、数据 2,3,4,5 的标准差是数据 4,6,8,10 的标准差的一半 |
| D、频率分布直方图中各小长方形的面积等于相应各组的频数 |
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为H.则以下命题中,错误的命题是( )
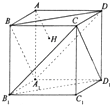

| A、点H是△A1BD的垂心 |
| B、AH垂直平面CB1D1 |
| C、直线AH和BB1所成角为45° |
| D、AH的延长线经过点C1 |
 某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),
某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),