题目内容
在平面直角坐标系上,设不等式组
所表示的平面区域为Dn,记Dn内的整点(即横坐标和纵坐标均为整数的点)的个数为an(n∈N*).则a1= ,经推理可得到an= .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:根据不等式组的解法,分别讨论x的取值,解出y的取值范围即可得到结论.
解答:
解:当n=1时,不等式为y≤-(x-3)=3-x,
当x=1时,y≤2,此时y=1,或y=2,
当x=2时,y≤1,此时y=1,
当x=3时,y≤0,此时不成立,
即a1=3.
由x>0,y>0,3n-nx>0,
得0<x<3,
∴x=1或x=2,
因此Dn内的整点在直线x=1或x=2上,记直线y=3n-nx为l,
l与直线x=1或x=2的交点的纵坐标分别为y1=1或y1=2,
则y1=3n-n=2n,y2=3n-2n=n,
∴an=2n+n=3n.
故答案为:3,3n.
当x=1时,y≤2,此时y=1,或y=2,
当x=2时,y≤1,此时y=1,
当x=3时,y≤0,此时不成立,
即a1=3.
由x>0,y>0,3n-nx>0,
得0<x<3,
∴x=1或x=2,
因此Dn内的整点在直线x=1或x=2上,记直线y=3n-nx为l,
l与直线x=1或x=2的交点的纵坐标分别为y1=1或y1=2,
则y1=3n-n=2n,y2=3n-2n=n,
∴an=2n+n=3n.
故答案为:3,3n.
点评:本题主要考查二元一次不等式组的应用,利用不等式的即可求出y的取值范围.

练习册系列答案
相关题目
图中表示的区域满足不等式( )
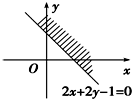

| A、2x+2y-1>0 |
| B、2x+2y-1≥0 |
| C、2x+2y-1≤0 |
| D、2x+2y-1<0 |
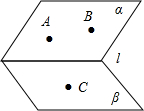 如图,已知平面α∩β=l,点A∈α,点B∈α,点C属于β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.
如图,已知平面α∩β=l,点A∈α,点B∈α,点C属于β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论. 某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),
某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),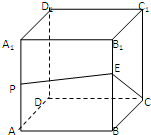 已知正方体ABCD-A1B1C1D1的棱长为2,P是AA1的中点,E是BB1上的点,则PE+EC的最小值是
已知正方体ABCD-A1B1C1D1的棱长为2,P是AA1的中点,E是BB1上的点,则PE+EC的最小值是