题目内容

已知|
a
|=1，|
b
|=2，向量
a
与
b
的夹角为60°，则|
a
+
b
|=（　　）
A、
5
B、
7
C、1
D、2
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意可得 
a
•
b
=1×2×cos60°=1，再根据|
a
+
b
|=
(
a
+
b
)2
=
a
2+b2+2
a
•
b
，计算求得结果
解答： 解：∵已知|
a
|=1，|
b
|=2，向量
a
与
b
的夹角为60°，
∴
a
•
b
=1×2×cos60°=1，
∴|
a
+
b
|=
(
a
+
b
)2
=
a
2+b2+2
a
•
b
=
7
，
故选：B．
点评：本题主要考查两个向量的数量积的定义，求向量的模，属于中档题．
练习册系列答案
相关题目
在极坐标系中，过点（3，
π
3
）且垂直于极轴的直线方程的极坐标方程是
 
（请选择正确标号填空）．（1）ρ=
3
2
sinθ；（2）ρ=
3
2
cosθ；（3）ρsinθ=
3
2
；（4）ρcosθ=
3
2
．
设a＞1．若曲线y=
1
x
与直线y=0，x=1，x=a，所围成封闭图形的面积为2，则a=
 
．
已知△ABC是正三角形，且它的边长为a，那么它的直观图△A′B′C′的面积为（　　）
A、
3
4
a2
B、
3
8
a2
C、
6
8
a2
D、
6
16
a2
图中表示的区域满足不等式（　　）
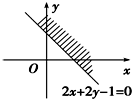
A、2x+2y-1＞0
B、2x+2y-1≥0
C、2x+2y-1≤0
D、2x+2y-1＜0
若双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的渐近线与抛物线x2=4y的准线所围成的三角形面积为2，则该双曲线的离心率为（　　）
A、
5
2
B、
2
C、
3
D、
5
下列说法中，正确的是（　　）
A、数据 5，4，4，3，5，2 的众数是 4
B、一组数据的标准差是这组数据的方差的平方
C、数据 2，3，4，5 的标准差是数据 4，6，8，10 的标准差的一半
D、频率分布直方图中各小长方形的面积等于相应各组的频数
已知集合A={0，1，2}，B={x-y|x∈A，y∈A}，则集合B中元素的个数为（　　）
A、3B、5C、7D、9
已知函数f（x）=lnx+
a
x+1
．
（1）当a=2时，证明对任意的x∈（1，+∞），f（x）＞1；
（2）求证：ln（n+1）＞
1
3
+
1
5
+
1
7
+…+
1
2n+1
（n∈N*）．
（3）若函数f（x）有且只有一个零点，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网