题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c,己知
=(cosA,
sinA),
=(2cosA,-2cosA),
•
=-1.
(Ⅰ)若a=2
,c=2,求△ABC的面积;
(Ⅱ)求
的值.
| m |
| 3 |
| n |
| m |
| n |
(Ⅰ)若a=2
| 3 |
(Ⅱ)求
| b-2c |
| acos(60°+C) |
考点:正弦定理,平面向量数量积的运算
专题:三角函数的求值
分析:(Ⅰ)由两向量的坐标及两向量数量积为-1,利用平面向量数量积运算法则计算列出关系式,再利用两角和与差的正弦函数公式化为一个角的正弦函数,确定出A的度数,由a与c的值,利用正弦定理求出sinC的值,即可确定出△ABC的面积;
(Ⅱ)原式利用正弦定理化简后,根据A的度数,得到B+C的度数,用C表示出B,代入关系式整理后约分即可得到结果.
(Ⅱ)原式利用正弦定理化简后,根据A的度数,得到B+C的度数,用C表示出B,代入关系式整理后约分即可得到结果.
解答:
解:(Ⅰ)∵
=(cosA,
sinA),
=(2cosA,-2cosA),
•
=-1.
∴2cos2A-2
sinAcosA=cos2A-
sin2A+1=-1,即-2(
sin2A-
cos2A)=-2,
∴sin(2A-
)=1,
∵A为三角形内角,
∴2A-
=
,即A=
,
∵a=2
,c=2,
∴由正弦定理
=
,
得:sinC=
=
=
,
∵C为三角形内角,∴C=
,
∴B=
,
则S△ABC=
×2×2
=2
;
(Ⅱ)∵
=
=
=2R,即a=2RsinA,b=2RsinB,c=2RsinC,
∴原式=
=
=
=
=
=2.
| m |
| 3 |
| n |
| m |
| n |
∴2cos2A-2
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
∴sin(2A-
| π |
| 6 |
∵A为三角形内角,
∴2A-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∵a=2
| 3 |
∴由正弦定理
| a |
| sinA |
| c |
| sinC |
得:sinC=
| csinA |
| a |
2×
| ||||
2
|
| 1 |
| 2 |
∵C为三角形内角,∴C=
| π |
| 6 |
∴B=
| π |
| 2 |
则S△ABC=
| 1 |
| 2 |
| 3 |
| 3 |
(Ⅱ)∵
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴原式=
| sinB-2sinC |
| sinAcos(60°+C) |
| sinB-2sinC | ||||
|
| sin(120°-C)-2sinC | ||||
|
| ||||||
|
| ||||
|
点评:此题考查了正弦定理,平面向量的数量积运算,两角和与差的正弦函数公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
图中表示的区域满足不等式( )
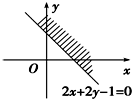

| A、2x+2y-1>0 |
| B、2x+2y-1≥0 |
| C、2x+2y-1≤0 |
| D、2x+2y-1<0 |
在锐角△ABC中,角A,B,C的对边分别为a,b,c.若ccosB+bcosC=2acosA,则角A为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为H.则以下命题中,错误的命题是( )
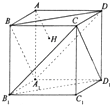

| A、点H是△A1BD的垂心 |
| B、AH垂直平面CB1D1 |
| C、直线AH和BB1所成角为45° |
| D、AH的延长线经过点C1 |
 如图是某高中十佳歌手比赛上某一位选手得分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为
如图是某高中十佳歌手比赛上某一位选手得分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为