题目内容
已知数列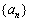 的首项
的首项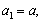 其中
其中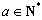 ,
,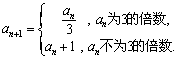
令集合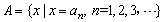 .
.
(I)若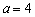 ,写出集合
,写出集合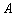 中的所有的元素;
中的所有的元素;
(II)若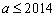 ,且数列
,且数列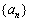 中恰好存在连续的7项构成等比数列,求
中恰好存在连续的7项构成等比数列,求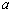 的所有可能取值构成的集合;
的所有可能取值构成的集合;
(III)求证: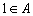 .
.
解:(I)集合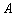 的所有元素为:4,5,6,2,3,1..
的所有元素为:4,5,6,2,3,1..
(II)不妨设成等比数列的这连续7项的第一项为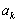 ,
,
如果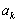 是3的倍数,则
是3的倍数,则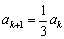 ;如果
;如果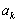 是被3除余1,则由递推关系可得
是被3除余1,则由递推关系可得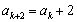 ,所以
,所以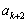 是3的倍数,所以
是3的倍数,所以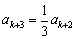 ;如果
;如果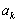 被3除余2,则由递推关系可得
被3除余2,则由递推关系可得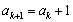 ,所以
,所以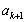 是3的倍数,所以
是3的倍数,所以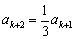 .
.
所以,该7项的等比数列的公比为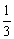 .
.
又因为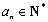 ,所以这7项中前6项一定都是3的倍数,而第7项一定不是3的倍数(否则构成等比数列的连续项数会多于7项),
,所以这7项中前6项一定都是3的倍数,而第7项一定不是3的倍数(否则构成等比数列的连续项数会多于7项),
设第7项为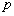 ,则
,则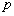 是被3除余1或余2的正整数,则可推得
是被3除余1或余2的正整数,则可推得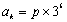
因为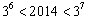 ,所以
,所以 或
或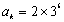 .
.
由递推关系式可知,在该数列的前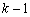 项中,满足小于2014的各项只有:
项中,满足小于2014的各项只有:
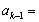
 或
或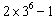 ,
,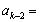
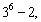 或
或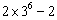 ,
,
所以首项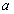 的所有可能取值的集合为
的所有可能取值的集合为
{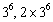 ,
,
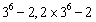 }.
}.
(III)若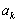 被3除余1,则由已知可得
被3除余1,则由已知可得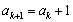 ,
,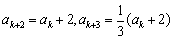 ;
;
若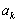 被3除余2,则由已知可得
被3除余2,则由已知可得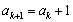 ,
,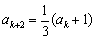 ,
, ;
;
若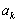 被3除余0,则由已知可得
被3除余0,则由已知可得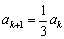 ,
,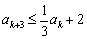 ;
;
所以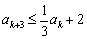 ,
,
所以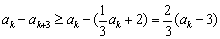
所以,对于数列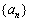 中的任意一项
中的任意一项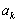 ,“若
,“若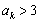 ,则
,则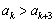 ”.
”.
因为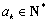 ,所以
,所以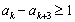 .
.
所以数列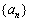 中必存在某一项
中必存在某一项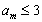 (否则会与上述结论矛盾!)
(否则会与上述结论矛盾!)
若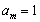 ,结论得证.
,结论得证.
若 ,则
,则 ;若
;若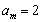 ,则
,则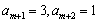 ,
,
所以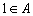 .
.

练习册系列答案
相关题目
 被椭圆
被椭圆 所截得的线段的中点,则
所截得的线段的中点,则 B.
B.
 D.
D.
 ,
, 是函数
是函数 图象上不同于
图象上不同于 的一点.有如下结论:
的一点.有如下结论: 是等腰三角形;
是等腰三角形; .
. 的最小正周期;
的最小正周期; 上的取值范围.
上的取值范围. 若目标函数z=ax+by(a>0,
若目标函数z=ax+by(a>0, +
+ 的最小值为( ).
的最小值为( ). B.
B. C.
C. D.4
D.4 ,目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是________.
,目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是________. ,
, .若
.若 使
使 则角C的大小为
则角C的大小为 B.
B.  C.
C.  D.
D. 