题目内容
设函数y=f(x)的导函数为f′(x),若y=f(x)的图象在点P(0,f(0))处的切线方程为2x-y+2=0,则f(0)+f′(0)的值为( )
| A、1 | B、2 | C、3 | D、4 |
考点:导数的运算
专题:导数的概念及应用
分析:根据导数的几何意义,即可得到结论.
解答:
解;∵y=f(x)的图象在点P(0,f(0))处的切线方程为2x-y+2=0,即y=2x+2,
∴切线斜率k=f′(0)=2,f(0)=2,
则f(0)+f′(0)=2+2=4,
故选:D
∴切线斜率k=f′(0)=2,f(0)=2,
则f(0)+f′(0)=2+2=4,
故选:D
点评:本题主要考查函数值计算,根据导数的几何意义求出相应的切线斜率是解决本题的关键.比较基础.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知定义在R上的偶函数f(x)满足f(x-1)=f(x+1),当0≤x≤1时,f(x)=x2,如果函数g(x)=f(x)-(x+m)有两个零点,则实数m的值为( )
| A、2k(k∈Z) | ||
B、2k-
| ||
C、2K或2K+
| ||
D、2K或2K-
|
已知函数f(x)=x2+(m2-4)x+m是偶函数,g(x)=xm在(-∞,0)内单调递增,则实数m=( )
| A、2 | B、±2 | C、0 | D、-2 |
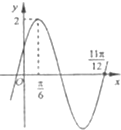 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)若x∈[-
| π |
| 2 |
“m=-2”是“直线mx+2y+2=0与直线2x+my+2=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
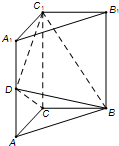 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=