题目内容
已知正三棱锥P-ABC的四个顶点都在半径为
的球面上，M，N分别为PA，AB的中点．若MN⊥CM，则球心到平面ABC的距离为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：由题意，可以把该正三棱锥看作为一个正方体的一部分，此正方体的体对角线为球的直径，球心为正方体对角线的中点，球心到截面ABC的距离为球的半径减去正三棱锥P-ABC在面ABC上的高，由此能求出球心到截面ABC的距离．
解答：
解：∵正三棱锥P-ABC的四个顶点都在半径为
的球面上，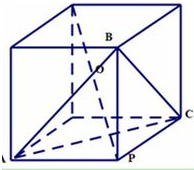
∴PA，PB，PC两两垂直，
∴可以把该正三棱锥看作为一个正方体的一部分，如右图，
此正方体的体对角线为球的直径，球心为正方体对角线的中点，
球心到截面ABC的距离为球的半径减去正三棱锥P-ABC在面ABC上的高，
∵球半径r=
，∴正方体的棱长为2，
∴正三棱锥P-ABC在面ABC上的高为
，
∴球心到截面ABC的距离为
-
=
．
故选：C．
| 3 |
∴PA，PB，PC两两垂直，∴可以把该正三棱锥看作为一个正方体的一部分，如右图，
此正方体的体对角线为球的直径，球心为正方体对角线的中点，
球心到截面ABC的距离为球的半径减去正三棱锥P-ABC在面ABC上的高，
∵球半径r=
| 3 |
∴正三棱锥P-ABC在面ABC上的高为
2
| ||
| 3 |
∴球心到截面ABC的距离为
| 3 |
2
| ||
| 3 |
| ||
| 3 |
故选：C．
点评：本题考查球心到平面的距离的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如果f（a+b）=f（a）•f（b）且f（1）=2，则
+
+
+…+
=（ ）
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(6) |
| f(5) |
| f(2014) |
| f(2013) |
| A、2012 | B、1007 |
| C、2014 | D、2013 |
设f（x），g（x）分别是定义在（-∞，0）∪（0，+∞）上的奇函数和偶函数，当x＜0时，f′（x）g（x）+f（x）g′（x）＞0．且g（-3）=0．则不等式f（x）g（x）＜0的解集是（ ）
| A、（-3，0）∪（3，+∞） |
| B、（-3，0）∪（0，3） |
| C、（-∞，-3）∪（3，+∞） |
| D、（-∞，-3）∪（0，3） |
如图是定义在区间[-2，2]的函数y=f（x），则f（x）的减区间是