题目内容
若tanα=2，则sin2α+2sinαcosα+3cos2α= ．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：利用同角三角函数的基本关系，把要求的式子化为
，再把tanα=2代入运算求得结果．
| tan2α+2tanα+3 |
| tan2α+1 |
解答：
解：sin2α+2sinαcosα+3cos2α=
=
，
=
=
，
故答案为：
．
| sin2α+2sinαcosα+3cos2α |
| sin2α+cos2α |
| tan2α+2tanα+3 |
| tan2α+1 |
=
| 4+4+3 |
| 4+1 |
| 11 |
| 5 |
故答案为：
| 11 |
| 5 |
点评：本题主要考查同角三角函数的基本关系的应用，属于基础题．
练习册系列答案
相关题目
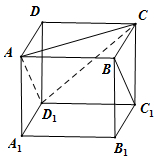如图，ABCD-A1B1C1D1为正方体，棱长为2．下面结论中正确的结论是