题目内容
已知函数f(x)=cos(2x+
)+cos2(
+x).
(1)求函数f(x)的单调递增区间.
(2)△ABC中,角A、B、C所对的边分别是a、b、c,且f(
)=-
,边c=2,∠C为锐角,△ABC的内切圆半径为
,求△ABC的面积.
| π |
| 3 |
| π |
| 2 |
(1)求函数f(x)的单调递增区间.
(2)△ABC中,角A、B、C所对的边分别是a、b、c,且f(
| c |
| 2 |
| 1 |
| 4 |
| ||
| 3 |
考点:余弦定理,三角函数中的恒等变换应用
专题:解三角形
分析:(1)函数解析式利用诱导公式变形,再利用两角和与差的余弦函数公式化简,整理后得到一个角的正弦函数,利用正弦函数的单调性即可确定出f(x)的得到递增区间;
(2)由f(
)=-
,求出C的度数,再由c的值,利用余弦定理列出关系式,记作①,利用三角形面积公式列出关系式,记作②,联立①②求出a+b的值,即可确定出三角形ABC的面积.
(2)由f(
| C |
| 2 |
| 1 |
| 4 |
解答:
解:(1)f(x)=cos(2x+
)+cos2(
+x)=cos(2x+
)+sin2x=
cos2x-
sin2x+
=
-
sin2x,
由2kπ+
≤x≤2kπ+
(k∈Z),得函数f(x)的单调递增区间为[2kπ+
,2kπ+
](k∈Z);
(2)∵f(
)=-
,
∴f(
)=
-
sinC=-
,即
sinC=
,
∴sinC=
,
∵∠C为锐角,
∴C=
.
∵c=2,
∴由余弦定理得c2=a2+b2-2abcos
=a2+b2-ab=(a+b)2-3ab=4①,
∴S△ABC=
absinC=
(a+b+c)r,r为内切圆半径,
∴
ab=
(a+b+2),
整理得:3ab=2(a+b+2)②,
②代入①得:(a+b)2-2(a+b)-8=0,
即(a+b-4)(a+b+2)=0,
解得:a+b=4或a+b=-2(舍去),
则S△ABC=
×(4+2)×
=
.
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
由2kπ+
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
(2)∵f(
| C |
| 2 |
| 1 |
| 4 |
∴f(
| C |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| 3 |
| 4 |
∴sinC=
| ||
| 2 |
∵∠C为锐角,
∴C=
| π |
| 3 |
∵c=2,
∴由余弦定理得c2=a2+b2-2abcos
| π |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| ||
| 2 |
| ||
| 3 |
整理得:3ab=2(a+b+2)②,
②代入①得:(a+b)2-2(a+b)-8=0,
即(a+b-4)(a+b+2)=0,
解得:a+b=4或a+b=-2(舍去),
则S△ABC=
| 1 |
| 2 |
| ||
| 3 |
| 3 |
点评:此题考查了余弦定理,三角形的面积公式,以及正弦函数的单调性,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 如图所示,空间中有一直角三角形POA,∠O为直角,OA=4,PO=3,现以其中一直角边PO为轴,按逆时针方向旋转60°后,将A点所在的位置记为B,再按逆时针方向继续旋转120°后,A点所在的位置记为C.
如图所示,空间中有一直角三角形POA,∠O为直角,OA=4,PO=3,现以其中一直角边PO为轴,按逆时针方向旋转60°后,将A点所在的位置记为B,再按逆时针方向继续旋转120°后,A点所在的位置记为C.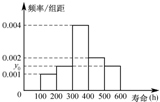 对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如图.
对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如图.