题目内容
设等差数列{an}的前n项和为Sn,且a4-a2=8,S10=190
(1)求数列{an}的通项公式;
(2)设p,q∈N+,试判断ap•aq是否仍为数列{an}中的项,并说明理由.
(1)求数列{an}的通项公式;
(2)设p,q∈N+,试判断ap•aq是否仍为数列{an}中的项,并说明理由.
考点:等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件列式求出等差数列{an}的首项和公差,直接代入等差数列的通项公式得答案;
(2)在等差数列的通项公式中取n=p,q,作积后得到ap•aq=4[4pq-3(p+q)+3]-3,判出4pq-3(p+q)+3∈N+得答案.
(2)在等差数列的通项公式中取n=p,q,作积后得到ap•aq=4[4pq-3(p+q)+3]-3,判出4pq-3(p+q)+3∈N+得答案.
解答:
解:(1)在等差数列{an}中,设首项为a1,公差为d,
∵a4-a2=8,
∴2d=8,d=4.
又S10=10a1+
d=10a1+
×4=190,
解得:a1=1.
故等差数列通项公式为:an=a1+(n-1)d=1+4(n-1)=4n-3;
(2)ap•aq=(4p-3)(4q-3)=16pq-12(p+q)+9=4[4pq-3(p+q)+3]-3,
∵p,q∈N+,
∴4pq-3(p+q)+3∈N+,
∴ap•aq是数列{an}中的项.
∵a4-a2=8,
∴2d=8,d=4.
又S10=10a1+
| 10(10-1) |
| 2 |
| 10(10-1) |
| 2 |
解得:a1=1.
故等差数列通项公式为:an=a1+(n-1)d=1+4(n-1)=4n-3;
(2)ap•aq=(4p-3)(4q-3)=16pq-12(p+q)+9=4[4pq-3(p+q)+3]-3,
∵p,q∈N+,
∴4pq-3(p+q)+3∈N+,
∴ap•aq是数列{an}中的项.
点评:本题考查等差数列的通项公式,考查等差数列的性质,对于(2)的求解关键是对题意的理解,是中档题.

练习册系列答案
相关题目
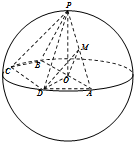 如图,平面四边形ABCD的四个顶点都在球O的表面上,AB为球O的直径,P为球面上一点,且PO⊥平面ABCD,NC=CD=DA=2,点M为PA的中点.
如图,平面四边形ABCD的四个顶点都在球O的表面上,AB为球O的直径,P为球面上一点,且PO⊥平面ABCD,NC=CD=DA=2,点M为PA的中点.