题目内容
18.在边长为4的等边三角形OAB内部任取一点P,使得$\overrightarrow{OA}$•$\overrightarrow{OP}$≤4的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{8}$ |
分析 设$\overrightarrow{OP}$在$\overrightarrow{OA}$上的投影为|OQ|,又$\overrightarrow{OA}$•$\overrightarrow{OP}$=|OA|•|OQ|,$\overrightarrow{OA}$•$\overrightarrow{OP}$≤4,则|OQ|≤1.
解答 解:如图,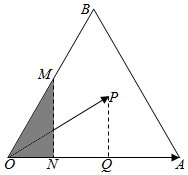
设$\overrightarrow{OP}$在$\overrightarrow{OA}$上的投影为|OQ|,又$\overrightarrow{OA}$•$\overrightarrow{OP}$=|OA|•|OQ|,$\overrightarrow{OA}$•$\overrightarrow{OP}$≤4,则|OQ|≤1;
即$\overrightarrow{OP}$在$\overrightarrow{OA}$上的投影小于等于1,作OP中点M,MN⊥OA于N,
∴满足条件的P的区域为上图阴影部分,N为OA四等分点,
∴使得$\overrightarrow{OA}$•$\overrightarrow{OP}$≤4的概率为:$\frac{{S}_{△OMN}}{{S}_{△OBA}}$=$\frac{1}{8}$,
故选:D.
点评 本题主要考查两个向量的数量积的定义,几何概型的概率问题,属于中档题

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
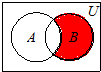
9.已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分的集合为( )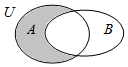

| A. | {x|-1<x<1} | B. | {x|1≤x<3} | C. | {x|x<3} | D. | {x|x≤-1} |
3.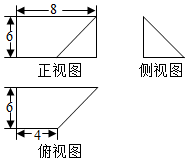 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )| A. | 72 | B. | 80 | C. | 120 | D. | 144 |
7.下列函数中,既是偶函数又在区间(1,2)内单调递减的是( )
| A. | f(x)=-cosx | B. | f(x)=2x+2-x | C. | f(x)=$\frac{1}{{x}^{2}}$ | D. | f(x)=$\sqrt{-x}$ |
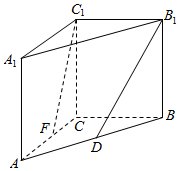 如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.