题目内容
9.已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分的集合为( )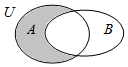
| A. | {x|-1<x<1} | B. | {x|1≤x<3} | C. | {x|x<3} | D. | {x|x≤-1} |
分析 由韦恩图中阴影部分表示的集合为A∩(∁RB),然后利用集合的基本运算进行求解即可.
解答 解:A={x|x2-2x-3<0}={x|-1<x<3},B={x|y=ln(1-x)}={x|1-x>0}={x|x<1},
则∁UB={x|x≥1},
由韦恩图中阴影部分表示的集合为A∩(∁UB),
∴A∩(∁UB)={x|1≤x<3},
故选:B.
点评 本题主要考查集合的基本运算,利用韦恩图确定集合关系,然后利用数轴求基本运算是解决此类问题的基本方法.

练习册系列答案
相关题目
4.等比数列{an}中,an>0,al+a2=6,a3=8,则a6=( )
| A. | 64 | B. | 128 | C. | 256 | D. | 512 |
14.已知$α∈(\frac{π}{2},π)$,$sinα=\frac{4}{5}$,则sin2α=( )
| A. | $-\frac{24}{25}$ | B. | $-\frac{7}{25}$ | C. | $\frac{7}{25}$ | D. | $\frac{24}{25}$ |
18.在边长为4的等边三角形OAB内部任取一点P,使得$\overrightarrow{OA}$•$\overrightarrow{OP}$≤4的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{8}$ |
19.为得到y=cos(2x-$\frac{π}{6}$)的图象,只需要将y=sin2x的图象( )
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
 如图,在平面直角坐标系xOy中,∠CAB=60°,AC=2,BC=$\sqrt{7}$.
如图,在平面直角坐标系xOy中,∠CAB=60°,AC=2,BC=$\sqrt{7}$.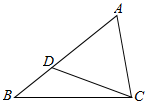 如图,在△ABC中,cosB=$\frac{11}{14}$,BC=7,点D在边AB上,且BD=3.
如图,在△ABC中,cosB=$\frac{11}{14}$,BC=7,点D在边AB上,且BD=3.