题目内容
18.函数$f(x)=\frac{sinx}{x}$的部分图象大致为( )| A. | 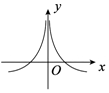 | B. |  | C. |  | D. |  |
分析 先根据函数的奇偶性的定义得到f(x)为偶函数,再根据极限的定义可得$\underset{lim}{x→0}$$\frac{sinx}{x}$=1,问题得以解决.
解答 解:函数的定义域为(-∞,0)∪(0,+∞),
∵f(-x)=$\frac{sin(-x)}{-x}$=$\frac{sinx}{x}$=f(x),
∴f(x)为偶函数,
∴f(x)的图象关于y轴对称,
∵$f(x)=\frac{sinx}{x}$,
∴$\underset{lim}{x→0}$$\frac{sinx}{x}$=$\underset{lim}{x→0}$cosx=cos0=1,
故选:B
点评 本题考查了函数图象的识别和应用,关键是掌握$\underset{lim}{x→0}$$\frac{sinx}{x}$=1,属于中档题.

练习册系列答案
相关题目
8.如果方程Ax+By+C=0表示的直线是x轴,则A、B、C满足( )
| A. | A•C=0 | B. | B≠0 | C. | B≠0且A=C=0 | D. | A•C=0且B≠0 |
9.在△ABC中,a=2,$B=\frac{π}{3}$,△ABC的面积等于$\frac{\sqrt{3}}{2}$,则b等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
18.甲、乙两人在一座9层大楼的地层进入电梯,若每个人直第二层开始在第一层离开电梯是等可能的,则2个人在不同楼层离开的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | $\frac{8}{9}$ | D. | $\frac{7}{8}$ |