题目内容
10.不等式选讲已知函数f(x)=|2x+a|-a(1)当a=2时,求不等式f(x)≤6的解集;
(2)设函数g(x)=|2x-1|,当x∈R时f(x)+g(x)≥3,求a的取值范围.
分析 (1)当a=2时,解不等式|2x+2|-2≤6得-5≤x≤3,即可求不等式f(x)≤6的解集;
(2)当x∈R时,f(x)+g(x)=|2x+a|-a+|2x-1|≥|2x+a+1-2x|-a=|a+1|-a,当$x=\frac{1}{2}$时等号成立,所以当x∈R时f(x)+g(x)≥3等价于|a+1|-a≥3,即可求a的取值范围.
解答 解:(1)当a=2时,f(x)=|2x+2|-2
解不等式|2x+2|-2≤6得-5≤x≤3
因此不等式f(x)≤6的解集为{x|-5≤x≤3}…(5分)
(2)当x∈R时,f(x)+g(x)=|2x+a|-a+|2x-1|≥|2x+a+1-2x|-a=|a+1|-a
当$x=\frac{1}{2}$时等号成立,所以当x∈R时f(x)+g(x)≥3等价于|a+1|-a≥3
当a≤-1时,a≤-2
当a>-1时,无解,
所以a∈(-∞,-2]…(10分)
点评 本题考查绝对值不等式的解法,考查绝对值不等式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
20.自主招生,是高校选拔录取工作改革的重要环节,通过高考自主招生笔试和面试之后,可以得到相应的高考降分政策;某高中高一学生共有1000人,其中城填初中毕业生750名(称为“城填生“),农村初中毕业生250人(称为“农村生“);为了摸清学生是否愿意参加自主招生,以便安排自主招生培训,拟采用分层抽样的方法抽取100名学生进行调查;
(1)试完成下列2×2联表,并分析是否有95%以上的把握说“是否愿意参加自主招生“与生源有关.
(2)现对愿意参加自主招生的同学组织摸底考试,考试题共有5道题,每题20分,对于这5道题,考生“高富帅”完全会答的有3道,不完全会的有2道,不完全会的每道题她得分S的概率满足:SKIPIF 1<0,假设解答各题之间没有影响.
①对于一道不完全会的题,求“高富帅”得分的均值E(s);
②试求“高富帅”在本次摸底考试中总得分的数学期望.
参考数据:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
(1)试完成下列2×2联表,并分析是否有95%以上的把握说“是否愿意参加自主招生“与生源有关.
| 愿意参加 | 不愿意参加 | 合计 | |
| 城填生 | 50 | 25 | 75 |
| 农村生 | 10 | 15 | 25 |
| 合计 | 60 | 40 | 100 |
①对于一道不完全会的题,求“高富帅”得分的均值E(s);
②试求“高富帅”在本次摸底考试中总得分的数学期望.
参考数据:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
1.“数列{an}为等比数列”是“${a_{n+1}}^2={a_n}•{a_{n+2}}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.若A(1,2),B(2,3),C(-3,5),则△ABC为( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 不等边三角形 |
9.如图,平行四边形ABCD的两条对角线相交于点M,且$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{MD}$=( )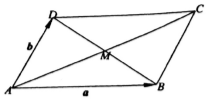

| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ |