Question

3．在△ABC中，AB=AC，D为BC边上一点，E为AD上一点，且满足∠BDE=2∠CED=∠BAC．求证：BD=2CD．

Answer 1

分析 作DO∥AB交AC于O，取F为△EDC的外接圆与AC的交点，利用△ADO∽△ABE，即得$\frac{OD}{AE}=\frac{AD}{AB}=\frac{AD}{AC}=\frac{AF}{AE}$，即可得出结论．

解答 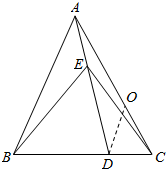证明：作DO∥AB交AC于O．
则由AB=AC易知OD=OC，且∠DOC=∠A=2∠CED，
所以O为△EDC的外心，
取F为△EDC的外接圆与AC的交点，则OF=OC=OD，∠ACE=∠ADF．
所以△ACE∽△ADF，即有AD/AC=AF/AE．
再由DO∥AB，∠ADO=∠BAE，∠AOD=180-∠DOC=180°-∠A=180°-∠BED=∠AEB，
所以△ADO∽△ABE，即得$\frac{OD}{AE}=\frac{AD}{AB}=\frac{AD}{AC}=\frac{AF}{AE}$．
故AF=OD=OC=CF，从而AO=2OC．
由DO∥AB得：BD=2CD．

点评 本题考查三角形相似的证明，考查比例的性质，考查学生分析解决问题的能力，属于中档题．