题目内容
18. 定义[x]表示不超过x的最大整数,例如[2.11]=2,[-1.39]=-2,执行如下图所示的程序框图,则输出m的值为
定义[x]表示不超过x的最大整数,例如[2.11]=2,[-1.39]=-2,执行如下图所示的程序框图,则输出m的值为( )
| A. | $\frac{19}{3}$ | B. | $\frac{53}{8}$ | C. | $\frac{171}{6}$ | D. | $\frac{185}{8}$ |
分析 模拟程序的运行,依据程序逐级运算,并通过判断条件n<7?调整运算的继续与结束,即可计算得解.
解答 解:模拟程序的运行,可得
m=3,n=1
[3]=3为奇数,m=$\frac{19}{3}$,n=3
满足条件n<7,执行循环体,[$\frac{19}{3}$]=6不为奇数,m=$\frac{13}{2}$,n=5
满足条件n<7,执行循环体,[$\frac{13}{2}$]=6不为奇数,m=$\frac{53}{8}$,n=7
不满足条件n<7,退出循环,输出m的值为$\frac{53}{8}$.
故选:B.
点评 本题考查程序框图的运算和对不超过x的最大整数[x]的理解.要得到该程序运行后输出的S的值,主要依据程序逐级运算,并通过判断条件n<7?调整运算的继续与结束,注意执行程序运算时的顺序,本题属于基本知识的考查.

练习册系列答案
相关题目
8.如果实数x,y满足约束条件$\left\{\begin{array}{l}{2x+y-4≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$,则z=3x+2y+$\frac{y}{x}$的最大值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 11 |
9.已知$\overrightarrow{OA}$=(cos2x,-1),$\overrightarrow{OB}$=(1,sin2x+$\sqrt{3}$sin2x)(x∈R),若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OB}$,则函数f(x)的最小正周期( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
6.已知直线l与平面α相交但不垂直,m为空间内一条直线,则下列结论一定不成立的是( )
| A. | m⊥l,m?α | B. | m⊥l,m∥α | C. | m∥l,m∩α≠∅ | D. | m⊥l,m⊥α |
3.双曲线$\frac{y^2}{3}-{x^2}=1$的焦点坐标是( )
| A. | $(±\sqrt{2},0)$ | B. | $(0,±\sqrt{2})$ | C. | (0,±2) | D. | (±2,0) |
 某次数学测验,12名同学分数的茎叶图如图:则这些分数的中位数是80.
某次数学测验,12名同学分数的茎叶图如图:则这些分数的中位数是80.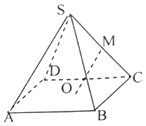 如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$.
如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$.