题目内容
13.已知(a$\sqrt{x}$+$\frac{\sqrt{3}}{x}$)6(a>0)展开式中的常数项是5,则a=$\frac{\sqrt{3}}{3}$.分析 利用二项式展开式的通项公式求出展开式的常数项的表达式,列方程求出a的值.
解答 解:(a$\sqrt{x}$+$\frac{\sqrt{3}}{x}$)6(a>0)展开式中,
通项公式为:
Tr+1=${C}_{6}^{r}$•${(a\sqrt{x})}^{6-r}$•${(\frac{\sqrt{3}}{x})}^{r}$=a6-r•${(\sqrt{3})}^{r}$•${C}_{6}^{r}$•${x}^{3-\frac{3r}{2}}$,
令3-$\frac{3r}{2}$=0,解得r=2;
∴展开式的常数项是a4•${(\sqrt{3})}^{2}$•${C}_{6}^{2}$=5,
解得a=±$\frac{\sqrt{3}}{3}$;
又a>0,∴a=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查了二项式展开式的通项公式与应用问题,是基础题.

练习册系列答案
相关题目
1.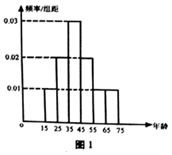 持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机选取了30人进行调查,将他们的年龄(单位:岁)数据绘制成频率分布直方图(图1),并将调查情况进行整理后制成表2:
持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机选取了30人进行调查,将他们的年龄(单位:岁)数据绘制成频率分布直方图(图1),并将调查情况进行整理后制成表2:
表2:
(Ⅰ)由于工作人员粗心,不小心将表2弄脏,遗失了部分数据,请同学们将表2中的数据恢复,并估计该市公众对“车辆限行”的赞成率和被调查者的年龄平均值;
(Ⅱ)把频率当作概率估计赞成车辆限行的情况,若从年龄在[55,65),[65,75]的被调查者中随机抽取一个人进行追踪调查,求被选2人中至少一个人赞成车辆限行的概率.
 持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机选取了30人进行调查,将他们的年龄(单位:岁)数据绘制成频率分布直方图(图1),并将调查情况进行整理后制成表2:
持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机选取了30人进行调查,将他们的年龄(单位:岁)数据绘制成频率分布直方图(图1),并将调查情况进行整理后制成表2:表2:
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 3 | 6 | 6 | 3 | ||
| 赞成人数 | 2 | 4 | 5 | 4 | 2 | 1 |
(Ⅱ)把频率当作概率估计赞成车辆限行的情况,若从年龄在[55,65),[65,75]的被调查者中随机抽取一个人进行追踪调查,求被选2人中至少一个人赞成车辆限行的概率.
8.若圆x2+y2+4x-2y-a2=0截直线x+y+5=0所得弦的长度为2,则实数a=( )
| A. | ±2 | B. | -2 | C. | ±4 | D. | 4 |
18. 定义[x]表示不超过x的最大整数,例如[2.11]=2,[-1.39]=-2,执行如下图所示的程序框图,则输出m的值为
定义[x]表示不超过x的最大整数,例如[2.11]=2,[-1.39]=-2,执行如下图所示的程序框图,则输出m的值为
( )
 定义[x]表示不超过x的最大整数,例如[2.11]=2,[-1.39]=-2,执行如下图所示的程序框图,则输出m的值为
定义[x]表示不超过x的最大整数,例如[2.11]=2,[-1.39]=-2,执行如下图所示的程序框图,则输出m的值为( )
| A. | $\frac{19}{3}$ | B. | $\frac{53}{8}$ | C. | $\frac{171}{6}$ | D. | $\frac{185}{8}$ |
5.已知点M(4,t)在抛物线x2=4y上,则点M到焦点的距离为( )
| A. | 5 | B. | 6 | C. | 4 | D. | 8 |
2.空间四边形OABC中,M,N分别是对边OA,BC的中点,点G为MN中点,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OG}$可以用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示为( )
| A. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ | D. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{c}$ |
3.已知x∈R,则“x>2”是“x2-3x+2>0”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |