题目内容
袋中装有m个红球和n个白球(m≥n≥2),这些红球和白球除了颜色不同之外,其余都相同,从袋中同时取出2个球,
(1)若取出的两个球都是红球的概率是取出的两个球是1红1白的概率的整数倍,试证:m必为奇数.
(2)若取出的球是同色球的概率等于取出不同色球的概率,试求适合m+n≤40的所有数组(m,n).
(1)若取出的两个球都是红球的概率是取出的两个球是1红1白的概率的整数倍,试证:m必为奇数.
(2)若取出的球是同色球的概率等于取出不同色球的概率,试求适合m+n≤40的所有数组(m,n).
考点:排列、组合的实际应用,古典概型及其概率计算公式
专题:
分析:(1)根据题意,先利用组合数公式计算出从“袋中任取2个”、“取出两个球都是红球”、“取出的两个球是1红1白”的取法数目,进而可以结合古典概型公式计算出“取出两个球都是红球”的概率与“取出的两个球是1红1白”的概率,又由题意可得有
=k(k∈Z),将其变形可得m=2kn+1,即可得证明;
(2)结合(1)中“取出的两个球是1红1白”的概率,由对立事件的概率性质可得“取出球是同色球”的概率,结合题意分析可得
=
,变形可得(m-n)2=m+n,
即m+n为完全平方数,进而可以确定m+n的范围,即可得m+n的值,结合(m-n)2=m+n可得m、n的值,综合可得答案.
| ||||||||
|
(2)结合(1)中“取出的两个球是1红1白”的概率,由对立事件的概率性质可得“取出球是同色球”的概率,结合题意分析可得
| ||||
|
| 1 |
| 2 |
即m+n为完全平方数,进而可以确定m+n的范围,即可得m+n的值,结合(m-n)2=m+n可得m、n的值,综合可得答案.
解答:
解:(1)证明:根据题意,
袋中装有m个红球和n个白球,从中任取2个,有
种不同的取法,
其中取出两个球都是红球的取法有
种,
取出的两个球是1红1白的取法有
•
种,
则取出两个球都是红球的概率为
,取出的两个球是1红1白的概率为
,
又由题意,取出的两个球都是红球的概率是取出的两个球是1红1白的概率的整数倍,
则有
=k(k∈Z),变形可得m=2kn+1,∵k∈Z,n∈N,∴m必为奇数;
(2)由(1)的结论,取出的两个球是1红1白即颜色不同的概率为
,
则取出球是同色球的概率为1-
,
又由取出的球是同色球的概率等于取出不同色球的概率,则有
=
,
变形可得(m-n)2=m+n,
即m+n为完全平方数,
又m+n≤40且m≥n≥2,
则4<m+n≤40且m+n为完全平方数;
则m+n=36或25或16或9,
m+n=36时,(m-n)2=36,即m-n=6,解可得m=21、n=15,
m+n=25时,(m-n)2=25,即m-n=5,解可得m=15、n=10,
m+n=16时,(m-n)2=16,即m-n=4,解可得m=10、n=6,
m+n=9时,(m-n)2=9,即m-n=,解可得m=6、n=3,
符合题意的数组共四组(m,n),结果为(21,15),(15,10),(10,6),(6,3).
袋中装有m个红球和n个白球,从中任取2个,有
| C | 2 m+n |
其中取出两个球都是红球的取法有
| C | 2 m |
取出的两个球是1红1白的取法有
| C | 1 m |
| C | 1 n |
则取出两个球都是红球的概率为
| ||
|
| ||||
|
又由题意,取出的两个球都是红球的概率是取出的两个球是1红1白的概率的整数倍,
则有
| ||||||||
|
(2)由(1)的结论,取出的两个球是1红1白即颜色不同的概率为
| ||||
|
则取出球是同色球的概率为1-
| ||||
|
又由取出的球是同色球的概率等于取出不同色球的概率,则有
| ||||
|
| 1 |
| 2 |
变形可得(m-n)2=m+n,
即m+n为完全平方数,
又m+n≤40且m≥n≥2,
则4<m+n≤40且m+n为完全平方数;
则m+n=36或25或16或9,
m+n=36时,(m-n)2=36,即m-n=6,解可得m=21、n=15,
m+n=25时,(m-n)2=25,即m-n=5,解可得m=15、n=10,
m+n=16时,(m-n)2=16,即m-n=4,解可得m=10、n=6,
m+n=9时,(m-n)2=9,即m-n=,解可得m=6、n=3,
符合题意的数组共四组(m,n),结果为(21,15),(15,10),(10,6),(6,3).
点评:本题考查古典概型的计算,涉及排列、组合的应用,关键是正确运用排列、组合公式,准确计算出各个事件的概率.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
如图,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则BE=( )
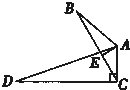

| A、3 | ||
| B、4 | ||
C、4
| ||
| D、5 |
已知i是虚数单位,则复数z=
所对应的点落在( )
| i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
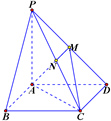 如图,已知四棱锥P-ABCD的底面是边长为2的正方形,PA⊥底面ABCD,且PA=AD,点M、N分别为侧棱PD、PC的中点.
如图,已知四棱锥P-ABCD的底面是边长为2的正方形,PA⊥底面ABCD,且PA=AD,点M、N分别为侧棱PD、PC的中点.