题目内容

盒中装有5个产品，其中3个一等品，2个二等品，从中不放回地取产品，每次1个，求：
（1）取两次，两次都取得一等品的概率；
（2）取两次，第二次取得一等品的概率；
（3）取三次，第三次才取得一等品的概率；
（4）取两次，已知第二次取得一等品，求第一次取得是二等品的概率．
考点：古典概型及其概率计算公式
专题：计算题,概率与统计
分析：首先确定都是古典概型，依次求概率即可．
解答： 解：（1）取两次，两次都取得一等品的概率P=
c
2
3
c
2
5
=
3
10
；
（2）取两次，第二次取得一等品的概率P=
c
1
3
c
1
5
=
3
5
；
（3）取三次，第三次才取得一等品的概率P=
c
1
2
•c
1
1
•
c
1
3
A
3
5
=
1
10
；
（4）取两次，已知第二次取得一等品，求第一次取得是二等品的概率P=
c
1
2
c
1
4
=
1
2
．
点评：本题考查了古典概型概率公式的应用，属于基础题．
练习册系列答案
相关题目
点（1，-1）到直线3x-4y+3=0的距离为（　　）
A、2
B、1
C、
2
5
D、
6
5
（1）高中课程中，在各个领域我们学习许多知识．在语言与文学领域，学习语文和外语；在数学领域学习数学；在人文与社会领域，学习思想政治、历史和地理；在科学领域，学习物理、化学和生物；在技术领域，学习通用技术和信息技术；在艺术领域学习音乐、美术和艺术；在体育与健康领域，学习体育等．试设计一个学习知识结构图．
（2）在选举过程中常用差额选举（候选人数多于当选人数）．某班选举班长，具体方法是：筹备选举，由班主任提名候选人，同学投票，验票统计，若得票多者，则选为班长；若票数相同则由班主任决定谁当选．请用流程图表示该选举的过程．
袋中装有m个红球和n个白球（m≥n≥2），这些红球和白球除了颜色不同之外，其余都相同，从袋中同时取出2个球，
（1）若取出的两个球都是红球的概率是取出的两个球是1红1白的概率的整数倍，试证：m必为奇数．
（2）若取出的球是同色球的概率等于取出不同色球的概率，试求适合m+n≤40的所有数组（m，n）．
设复数z=
(1+i)2+3(1-i)
2+i
，若az+b=1+i，求实数a，b的值．
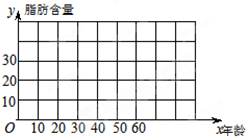在关于人体脂肪含量y（百分比）和年龄x关系的研究中，得到如下一组数据
年龄x232739414550
脂肪含量y9.517.821.225.927.528.2
（Ⅰ）画出散点图，判断x与y是否具有相关关系；
（Ⅱ）通过计算可知
b
=0.6512，
a
=-2.72，请写出y对x的回归直线方程，并计算出23岁和50岁的残差．
在△ABC中，内角A，B，C所对的分别是a，b，c，已知a=2，c=
2
，cosA=-
2
4
；
（Ⅰ）求sinC和b的值；    
（Ⅱ）求cos（2A-
π
3
）的值．
某食品加工厂甲，乙两个车间包装小食品，在自动包装传送带上每隔30分钟抽取一袋食品，称其重量并将数据记录如下：
甲：102  100  98  97  103  101  99
乙：102  101  99  98  103  98   99
（1）食品厂采用的是什么抽样方法（不必说明理由）？
（2）根据数据估计这两个车间所包装产品每袋的平均质量；
（3）分析哪个车间的技术水平更好些？
附：S=
1
n
[(x1-
.
x
)2+(x2-
.
x
)2+…+(xn-
.
x
)n]
．
已知三点A（1，3），B（5，11），C（-3，-5），求证：这三点在同一条直线上．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网