题目内容
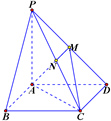 如图,已知四棱锥P-ABCD的底面是边长为2的正方形,PA⊥底面ABCD,且PA=AD,点M、N分别为侧棱PD、PC的中点.
如图,已知四棱锥P-ABCD的底面是边长为2的正方形,PA⊥底面ABCD,且PA=AD,点M、N分别为侧棱PD、PC的中点.(1)求证:CD∥平面AMN;
(2)求证:AM⊥平面PCD;
(3)求三棱锥C-AMN的体积.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)根据线面平行的判定定理,只要证明CD∥MN;
(2)根据线面垂直的判定定理,只要证明AM⊥PD,AM⊥CD即可;
(3)利用三棱锥的体积公式,只要求出三棱锥A-PCD的条件即可.
(2)根据线面垂直的判定定理,只要证明AM⊥PD,AM⊥CD即可;
(3)利用三棱锥的体积公式,只要求出三棱锥A-PCD的条件即可.
解答:
证明:(1)∵M,N分别是侧棱PD,PC的中点,
⇒CD∥面AMN;
(2)∵PA=AD,CD⊥DA,
∴AM⊥PD,
又
⇒CD⊥面PAD,
∵AM?PAD,
∴CD⊥AM,
又PD∩CD=D,
AM⊥面PCD;
(3)VC-AMN=VA-MNC=
SMNC•AM=
×
×
SPCD•AM=
×
SPCD•AM=
×
×
×2×2
×
=
.
|
(2)∵PA=AD,CD⊥DA,
∴AM⊥PD,
又
|
∵AM?PAD,
∴CD⊥AM,
又PD∩CD=D,
AM⊥面PCD;
(3)VC-AMN=VA-MNC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
点评:本题考查了空间线面关系,利用判定定理判定线面平行和线面垂直.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
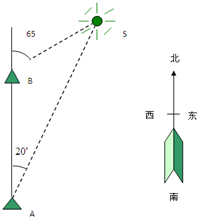 如图,一艘船以32.2n mile/h的速度向正北航行.在A处看灯塔S在船的北偏东20°的方向,30min后航行到B处,在B处看灯塔在船的北偏东65°的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
如图,一艘船以32.2n mile/h的速度向正北航行.在A处看灯塔S在船的北偏东20°的方向,30min后航行到B处,在B处看灯塔在船的北偏东65°的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?