题目内容
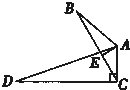
如图,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则BE=( )

| A、3 | ||
| B、4 | ||
C、4
| ||
| D、5 |
考点:解三角形
专题:计算题,解三角形
分析:先在△ACD中计算cos∠D,再在△ABE中,计算cos∠B,即可得到结论.
解答:
解:在△ACD中,AC=4,AD=12,∠ACD=90°,∴DC=8
∴cos∠D=
=
,
∵∠B=∠D,AE⊥BC,AB=6,
∴cos∠B=
∴
=
∴BE=4
故选:C.
| 2 |
∴cos∠D=
8
| ||
| 12 |
2
| ||
| 3 |
∵∠B=∠D,AE⊥BC,AB=6,
∴cos∠B=
| BE |
| AB |
∴
2
| ||
| 3 |
| BE |
| 6 |
∴BE=4
| 2 |
故选:C.
点评:本题考查三角函数的运用,解题的关键是正确运用余弦函数,属于基础题.

练习册系列答案
相关题目
已知集合M={1,2,3},N={-2,2},下列判断正确的是( )
| A、N⊆M |
| B、M∪N=M |
| C、M∩N=N |
| D、M∩N={2} |
已知平面向量
=(m,3),
=(1,-2),
+
与
垂直,则m=( )
| a |
| b |
| a |
| b |
| b |
| A、-1 | B、1 | C、-2 | D、2 |
一个正方体的顶点都在球面上,且它的棱长为a,则球的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,若
=
,那么△ABC一定是( )
| b2 |
| a2 |
| tanB |
| tanA |
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、直角三角形或等腰三角形 |
点(1,-1)到直线3x-4y+3=0的距离为( )
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
已知函数f(x)=ax3+bx2+cx+d(a≠0),则下列情况不可能出现的是( )
| A、f(x)有两个极值点,且极大值点大于极小值点 |
| B、f(x)有两个极值点,且极大值点小于极小值点 |
| C、f(x)有且只有一个极值点 |
| D、f(x)无极值点 |