题目内容
 如图为一半径为2的扇形(其中扇形中心角为90°),在其内部随机地撒一粒黄豆,则它落在阴影部分的概率为( )
如图为一半径为2的扇形(其中扇形中心角为90°),在其内部随机地撒一粒黄豆,则它落在阴影部分的概率为( )A、
| ||
B、
| ||
C、
| ||
D、1-
|
考点:几何概型
专题:概率与统计
分析:求出扇形的面积和阴影部分的面积,结合几何概型的计算公式即可求得黄豆落在阴影区域内的概率.
解答:
解:扇形的半径为2,则S扇形=
π22=π,
三角形的面积为:S三角形=
×22=2
则黄豆落在阴影区域的概率P=1-
=1-
.
故选D.
| 1 |
| 4 |
三角形的面积为:S三角形=
| 1 |
| 2 |
则黄豆落在阴影区域的概率P=1-
| S三角形 |
| S扇形 |
| 2 |
| π |
故选D.
点评:本小题主要考查扇形面积公式、几何概型等基础知识,考查运算求解能力,考查数形结合思想.关键是要求出阴影部分的面积及正方形的面积.属于基础题.

练习册系列答案
相关题目
函数f(x)=-2x2-x+1,x∈[-3,1]的最大值与最小值的和为( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
若点M是△ABC所在平面内的一点,且满足|3
-
-
|=0,则△ABM与△ABC面积之比等于( )
| AM |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
从数字1,2,3,4,5中任取3个,组成没有重复数字的三位数中是奇数的概率( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在边长为1的正方形中随机撒1000粒豆子,有230粒落在阴影部分,据此估计阴影部分的面积为
如图,在边长为1的正方形中随机撒1000粒豆子,有230粒落在阴影部分,据此估计阴影部分的面积为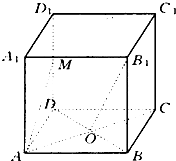 在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点.
在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点.