题目内容
18.定义在R上的函数f(x)的导函数为f′(x),且f(x)+xf′(x)<xf(x)对x∈R恒成立,则( )| A. | 3f(3)>2ef(2) | B. | 3f(3)<2ef(2) | C. | f(2)>0 | D. | f(-2)>0 |
分析 构造g(x)=$\frac{xf(x)}{{e}^{x}}$,利用导数的运算法则及其已知可得:g′(x)=$\frac{f(x)+x{f}^{′}(x)-xf(x)}{{e}^{x}}$<0,即可得出.
解答 解:构造g(x)=$\frac{xf(x)}{{e}^{x}}$,则g′(x)=$\frac{f(x)+x{f}^{′}(x)-xf(x)}{{e}^{x}}$<0,
∴函数g(x)在R上单调递减.
∴$\frac{3f(3)}{{e}^{3}}$<$\frac{2f(2)}{{e}^{2}}$,
∴3f(3)<2ef(2),
故选:B.
点评 本题考查了利用导数研究函数的单调性、构造法、不等式的性质与解法,充分根据已知构造函数是解题的关键,考查了推理能力与计算能力,属于难题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
13.在平面直角坐标系中,角α的顶点与原点重合,始边与x轴的非负半轴重合,终边过点P(-$\sqrt{3}$,-1),sin($\frac{π}{2}$-2α)=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
3.设集合A={-1,1,2,3},集合B={-2,-1,0,1}则A∩B=( )
| A. | {-2,-1,1,2} | B. | {-1,1} | C. | {2} | D. | {1} |
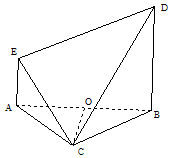 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.