题目内容
8.已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1、F2,A为椭圆E的右顶点,B,C分别为椭圆E的上、下顶点.线段CF2的延长线与线段AB交于点M,与椭圆E交于点P.(1)若椭圆的离心率为$\frac{{\sqrt{2}}}{2}$,△PF1C的面积为12,求椭圆E的方程;
(2)设S${\;}_{△CM{F}_{2}}$=λ•S${\;}_{△CP{F}_{1}}$,求实数λ的最小值.
分析 (1)由题意可知b=c,则△F1CF2是等腰直角三角形,利用勾股定理及椭圆的定义,求得丨PF1丨=$\frac{5a}{3}$,丨PF2丨=$\frac{a}{3}$,丨PC丨=$\frac{4a}{3}$,根据三角形的面积公式,即可求得椭圆E的方程;
(2)求得直线AB及PC的方程,联立求得M点坐标,由题意可知:丨CM丨=λ丨CP丨,根据向量数量积求得P点坐标,代入椭圆方程,利用基本不等式性质即可求得λ的最小值.
解答  解:(1)由椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,则a=$\sqrt{2}$c,b2=a2-c2=c2,
解:(1)由椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,则a=$\sqrt{2}$c,b2=a2-c2=c2,
∴△F1CF2是等腰直角三角形,丨PF1丨+丨PF2丨=2a,则丨PF2丨=2a-丨PF1丨,
由勾股定理知,丨PF1丨2=丨CF1丨2+丨CP丨2,丨PF1丨2=a2+(a+丨PF2丨2)2,
则丨PF1丨2=a2+(3a-丨PF1丨2)2,
解得:丨PF1丨=$\frac{5a}{3}$,丨PF2丨=$\frac{a}{3}$,丨PC丨=$\frac{4a}{3}$,
∴△PF1C的面积为S=$\frac{1}{2}$×a×$\frac{4a}{3}$=12,即a2=18,b2=9.
∴椭圆E的方程为$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{9}=1$;
(2)设P(x,y),因为直线AB的方程为y=-$\frac{b}{a}$x+b,直线PC的方程为y=$\frac{b}{c}$-b,
所以联立方程解得M($\frac{2ac}{a+c}$,$\frac{ab-bc}{a+c}$).
因为S${\;}_{△CM{F}_{2}}$=λ•S${\;}_{△CP{F}_{1}}$,所以丨CM丨=λ丨CP丨,所以$\overrightarrow{CM}$=λ$\overrightarrow{CP}$,
∴($\frac{2ac}{a+c}$,$\frac{ab-bc}{a+c}$)=λ(x,y+b),则x=$\frac{2ac}{λ(a+c)}$,y=$\frac{2ab-λb(a+c)}{a+c}$,
代入椭圆E的方程,得$\frac{4{c}^{2}}{{λ}^{2}(a+c)^{2}}$+$\frac{[2a-λ(a+c)]^{2}}{{λ}^{2}(a+c)^{2}}$=1,
即4c2+[2a-λ(a+c)]2=λ2(a+c)2,
∴λ=$\frac{{a}^{2}+{c}^{2}}{a(a+c)}$=$\frac{1+{e}^{2}}{1+e}$=1+e+$\frac{2}{1+e}$-2≥2$\sqrt{(1+e)×\frac{2}{1+e}}$-2=2$\sqrt{2}$-2,
因为0<e<1,1<e+1<2,
∴当且仅当e+1=$\sqrt{2}$,即e=$\sqrt{2}$-1时,
∴取到最小值2$\sqrt{2}$-2.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查基本不等式的应用,考查计算能力,属于中档题.

 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案| A. | 3f(3)>2ef(2) | B. | 3f(3)<2ef(2) | C. | f(2)>0 | D. | f(-2)>0 |
| A. | $-\frac{1}{2}$ | B. | 1 | C. | $-\frac{3}{5}$ | D. | $-\frac{7}{17}$ |
| A. | ?p | B. | q | C. | p∨(?q) | D. | (?p)∨q |
| A. | {x|-1<x≤0} | B. | {x|0≤x<4} | C. | {1,2,3} | D. | {0,1,2,3} |
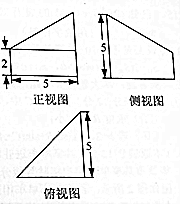 《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )
《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )| A. | 50 | B. | 75 | C. | 25.5 | D. | 37.5 |
| A. | a不能被2017整除 | B. | b不能被2017整除 | ||
| C. | a、b都不能被2017整除 | D. | a、b中至多有一个能被2017整除 |