题目内容
7.已知$\overrightarrow a=({1,λ}),\overrightarrow b=({2,1})$,若向量$2\overrightarrow a+\overrightarrow b$与$\overrightarrow c=({8,6})$共线,则$\overrightarrow a$在$\overrightarrow b$方向上的投影为$\frac{3\sqrt{5}}{5}$.分析 根据向量共线求出λ,计算$\overrightarrow{a}•\overrightarrow{b}$,代入投影公式即可.
解答 解:2$\overrightarrow{a}+\overrightarrow{b}$=(4,2λ+1),
∵$2\overrightarrow a+\overrightarrow b$与$\overrightarrow c=({8,6})$共线,
∴2λ+1=3,即λ=1.
∴$\overrightarrow{a}•\overrightarrow{b}$=2+λ=3,
∴$\overrightarrow a$在$\overrightarrow b$方向上的投影为|$\overrightarrow{a}$|•cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{3}{\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$.
故答案为:$\frac{3\sqrt{5}}{5}$.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
相关题目
18.定义在R上的函数f(x)的导函数为f′(x),且f(x)+xf′(x)<xf(x)对x∈R恒成立,则( )
| A. | 3f(3)>2ef(2) | B. | 3f(3)<2ef(2) | C. | f(2)>0 | D. | f(-2)>0 |
2.下列函数中,既是偶函数,又在(-∞,0)内单调递增的为( )
| A. | y=x4+2x | B. | y=2|x| | C. | y=2x-2-x | D. | $y={log_{\frac{1}{2}}}|x|-1$ |
19.若倾斜角为α的直线l与曲线y=x4相切于点(1,1),则cos2α-sin2α的值为( )
| A. | $-\frac{1}{2}$ | B. | 1 | C. | $-\frac{3}{5}$ | D. | $-\frac{7}{17}$ |
 如图,点C在以AB为直径的圆O上,PA垂直于圆O所在的平面,G为△AOC的重心.
如图,点C在以AB为直径的圆O上,PA垂直于圆O所在的平面,G为△AOC的重心.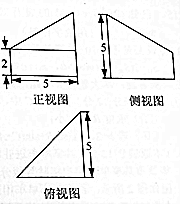 《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )
《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )