题目内容

计算∫
 
-1
-e
1
x
dx=
 
．
考点：定积分
专题：导数的概念及应用
分析：根据积分公式进行计算即可．
解答： 解：∵函数f（x）=
1
x
是奇函数，
∴根据奇函数的性质可知∫
 
-1
-e
1
x
dx=-
∫
e
1
1
x
dx=-lnx|
 
e
1
=-（lne-ln1）=-11．
故答案为：-1
点评：本题主要考查积分的计算，要求熟练掌握积分的几何意义和积分公式．
练习册系列答案
相关题目
已知集合M={x|
x
x+1
≥0，x∈R}，集合N={x||x|≤1，x∈R}，则M∩N=（　　）
A、{x|0＜x≤1}
B、{x|0≤x≤1}
C、{x1-1＜x≤1}
D、{x1-1＜x≤1}
已知定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M＞0，使得|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界．
下面我们来考虑两个函数：f（x）=4-x+p•2-x+1，g(x)=
1-q•2x
1+q•2x
．
（Ⅰ）当p=1时，求函数f（x）在（-∞，0）上的值域，并判断函数f（x）在（-∞，0）上是否为有界函数，请说明理由；
（Ⅱ）若q∈(
1
2
，
2
2
]，函数g（x）在[0，1]上的上界是H（q），求H（q）的取值范围；
（Ⅲ）若函数f（x）在[0，+∞）上是以3为上界的有界函数，求实数p的取值范围．
已知函数f（x）=loga（1-x）-loga（1+x），其中a＞0，且a≠1．
（1）判断f（x）的奇偶性；
（2）若f(
1
2
)=1，解不等式f（x）＜1．
为迎接2014年“马”年的到来，某校举办猜奖活动，参与者需先后回答两道选择题，问题A有三个选项，问题B有四个选项，但都只有一个选项是正确的，正确回答问题A可获奖金a元，正确回答问题B可获奖金b元．活动规定：参与者可任意选择回答问题的顺序，如果第一个问题回答正确，则继续答题，否则该参与者猜奖活动终止．假设一个参与者在回答问题前，对这两个问题都很陌生．
（Ⅰ）如果参与者先回答问题A，求其恰好获得奖金a元的概率；
（Ⅱ）试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大．
设A（1，0），B（0，1），直线l：y=ax，圆C：（x-a）2+y2=1．若圆C既与线段AB又与直线l有公共点，则实数a的取值范围是
 
．
设x，y∈R，若不等式组 
3x-y+2≥0
x-2y-2≤0
ax-y+1≥0
所表示的平面区域是一个锐角三角形，则a的取值范围是
 
．
直线y=x-1被椭圆x2+4y2=4截得的弦长为（　　）
A、
5
8
2
B、
8
5
2
C、3或
16
3
D、
2
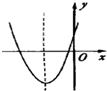二次函数y=ax2+bx+c的图象如图所示，则a+b+c
 
0；b2-4ac
 
0．（填“＞”或“＜”、“=”）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网