题目内容
已知定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,使得|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.
下面我们来考虑两个函数:f(x)=4-x+p•2-x+1,g(x)=
.
(Ⅰ)当p=1时,求函数f(x)在(-∞,0)上的值域,并判断函数f(x)在(-∞,0)上是否为有界函数,请说明理由;
(Ⅱ)若q∈(
,
],函数g(x)在[0,1]上的上界是H(q),求H(q)的取值范围;
(Ⅲ)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数p的取值范围.
下面我们来考虑两个函数:f(x)=4-x+p•2-x+1,g(x)=
| 1-q•2x |
| 1+q•2x |
(Ⅰ)当p=1时,求函数f(x)在(-∞,0)上的值域,并判断函数f(x)在(-∞,0)上是否为有界函数,请说明理由;
(Ⅱ)若q∈(
| 1 |
| 2 |
| ||
| 2 |
(Ⅲ)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数p的取值范围.
考点:函数的最值及其几何意义
专题:新定义
分析:(Ⅰ)根据有界函数的定义进行判断即可;
(Ⅱ)根据函数有界性的定义,求函数的最值即可求H(q)的取值范围;
(Ⅲ)根据函数f(x)在[0,+∞)上是以3为上界的有界函数,建立条件关系即可求实数p的取值范围.
(Ⅱ)根据函数有界性的定义,求函数的最值即可求H(q)的取值范围;
(Ⅲ)根据函数f(x)在[0,+∞)上是以3为上界的有界函数,建立条件关系即可求实数p的取值范围.
解答:
解:(1)当p=1时,f(x)=4-x+2-x+1
∵f(x)在(-∞,0)上递减,
∴f(x)>f(0)=3,
即f(x)在(-∞,1)的值域为(3,+∞).
故不存在常数M>0,使|f(x)|≤M成立,
∴函数f(x)在(-∞,1)上不是有界函数.
(2)g(x)=
-1,
∵q>0,x∈[0,1],
∴g(x)在[0,1]上递减,
∴g(1)≤g(x)≤g(0),
即
≤g(x)≤
.
∵q∈(
,
],
∴
≥-
,
∴|g(x)|≤
,
∴H(q)≥
,
即 [
,+∞)
(3)由题意知,|f(x)|≤3在[1,+∞)上恒成立.-3≤f(x)≤3,
∴-4•2x-(
)x≤p≤2•2x-(
)x在[0,+∞)上恒成立
∴[-4•2x-(
)x]max≤p≤[2•2x-(
)x]min
设2x=t,h(t)=-4t-
,p(t)=2t-
,
由x∈[0,+∞)得 t≥1,
设1≤t1<t2,h(t1)-h(t2)=
>0,
∴h(t)在[1,+∞)上递减,h(t)在[1,+∞)上的最大值为h(1)=-5,
又p(t1)-p(t2)=
<0,
∴p(t)在[1,+∞)上递增,p(t)在[1,+∞)上的最小值为p(1)=1.
∴实数p的取值范围为[-5,1].
∵f(x)在(-∞,0)上递减,
∴f(x)>f(0)=3,
即f(x)在(-∞,1)的值域为(3,+∞).
故不存在常数M>0,使|f(x)|≤M成立,
∴函数f(x)在(-∞,1)上不是有界函数.
(2)g(x)=
| 2 |
| 1+q•2x |
∵q>0,x∈[0,1],
∴g(x)在[0,1]上递减,
∴g(1)≤g(x)≤g(0),
即
| 1-2q |
| 1+2q |
| 1-q |
| 1+q |
∵q∈(
| 1 |
| 2 |
| ||
| 2 |
∴
| 1-q |
| 1+q |
| 1-2q |
| 1+2q |
∴|g(x)|≤
| 1-q |
| 1+q |
∴H(q)≥
| 1-q |
| 1+q |
即 [
| 1-q |
| 1+q |
(3)由题意知,|f(x)|≤3在[1,+∞)上恒成立.-3≤f(x)≤3,
∴-4•2x-(
| 1 |
| 2 |
| 1 |
| 2 |
∴[-4•2x-(
| 1 |
| 2 |
| 1 |
| 2 |
设2x=t,h(t)=-4t-
| 1 |
| t |
| 1 |
| t |
由x∈[0,+∞)得 t≥1,
设1≤t1<t2,h(t1)-h(t2)=
| (t2-t1)(4t1t2-1) |
| t1t2 |
∴h(t)在[1,+∞)上递减,h(t)在[1,+∞)上的最大值为h(1)=-5,
又p(t1)-p(t2)=
| (t1-t2)(2t1t2+1) |
| t1t2 |
∴p(t)在[1,+∞)上递增,p(t)在[1,+∞)上的最小值为p(1)=1.
∴实数p的取值范围为[-5,1].
点评:本题主要考查函数有界性的应用,利用函数有界性的定义是解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
定义在R上的函数f(x)=e|x|+x
,且f(x+t)>f(x)在x∈(-1,+∞)上恒成立,则关于x的方程f(x)=f(t)-e的根的个数叙述正确的是( )
| 4 |
| 3 |
| A、有两个 | B、有一个 |
| C、没有 | D、上述情况都有可能 |
过点M(-1,m),N(m+1,4)的直线的斜率等于1,则m的值为( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
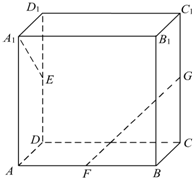 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成角的余弦值是( )
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成角的余弦值是( )