题目内容
设函数f(x)=x3+ax2-a2x-1,二次函数g(x)=ax2-x-1
(1)若a<0,求f(x)的单调区间;
(2)当函数y=f(x)与y=g(x)的图象只有一个公共点且g(x)存在最大值时,记g(x)的最大值为h(a),求函数h(a)的解析式;
(3)若函数f(x)与g(x)在区间(a-2,a)内均为增函数,求实数a的取值范围.
(1)若a<0,求f(x)的单调区间;
(2)当函数y=f(x)与y=g(x)的图象只有一个公共点且g(x)存在最大值时,记g(x)的最大值为h(a),求函数h(a)的解析式;
(3)若函数f(x)与g(x)在区间(a-2,a)内均为增函数,求实数a的取值范围.
考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:计算题,导数的综合应用
分析:(1)求导f′(x)=3x2+2ax-a2=3(x-
)(x+a),由导数的正负确定函数的单调性;
(2)由二次函数g(x)=ax2-x-1有最大值可得a<0,再由函数y=f(x)与y=g(x)的图象只有一个公共点可得-1≤a≤1,从而可得-1≤a<0,从而g(x)的最大值为h(a);
(3)分a正负讨论函数的单调区间,从而得到不等式组,从而求实数a的取值范围.
| a |
| 3 |
(2)由二次函数g(x)=ax2-x-1有最大值可得a<0,再由函数y=f(x)与y=g(x)的图象只有一个公共点可得-1≤a≤1,从而可得-1≤a<0,从而g(x)的最大值为h(a);
(3)分a正负讨论函数的单调区间,从而得到不等式组,从而求实数a的取值范围.
解答:
解:(1)f′(x)=3x2+2ax-a2=3(x-
)(x+a),
∵a<0,
∴
<-a,
故函数f(x)在区间(-∞,
),(-a,+∞)上单调递增,在(
,-a)上单调递减.
(2)∵二次函数g(x)=ax2-x-1有最大值,
∴a<0.
由f(x)=g(x)得x(x2-a2+1)=0,
∵函数y=f(x)与y=g(x)的图象只有一个公共点,
∴-a2+1≥0,
∴-1≤a≤1.
又∵a<0,
∴-1≤a<0.
又g(x)=a(x-
)2-
-1,
∴h(a)=-
-1,-1≤a<0.
(3)当a<0时,函数f(x)在区间(-∞,
)、(-a,+∞)上单调递增,函数g(x)在区间(-∞,
)上单调递增.
∴
,
解得a≤-
.
当a>0时,函数f(x)在区间(-∞,-a)、(
,+∞)上单调递增,函数g(x)在区间(
,+∞)上单调递增.
∴
,解得a≥3.
综上所述,实数a的取值范围是(-∞,-
]∪[3,+∞).
| a |
| 3 |
∵a<0,
∴
| a |
| 3 |
故函数f(x)在区间(-∞,
| a |
| 3 |
| a |
| 3 |
(2)∵二次函数g(x)=ax2-x-1有最大值,
∴a<0.
由f(x)=g(x)得x(x2-a2+1)=0,
∵函数y=f(x)与y=g(x)的图象只有一个公共点,
∴-a2+1≥0,
∴-1≤a≤1.
又∵a<0,
∴-1≤a<0.
又g(x)=a(x-
| 1 |
| 2a |
| 1 |
| 4a |
∴h(a)=-
| 1 |
| 4a |
(3)当a<0时,函数f(x)在区间(-∞,
| a |
| 3 |
| 1 |
| 2a |
∴
|
解得a≤-
| ||
| 2 |
当a>0时,函数f(x)在区间(-∞,-a)、(
| a |
| 3 |
| 1 |
| 2a |
∴
|
综上所述,实数a的取值范围是(-∞,-
| ||
| 2 |
点评:本题考查了函数的导数的综合应用,属于难题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
圆锥的母线长为6,轴截面的顶角为120度,过两条母线作截面,则截面面积的最大值为( )
A、9
| ||
| B、18 | ||
C、18
| ||
| D、9 |
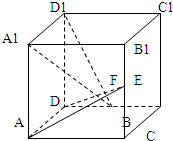 如果正方体ABCD-A1B1C1D1中EF分别是BB1、CD中点.
如果正方体ABCD-A1B1C1D1中EF分别是BB1、CD中点.